
【題目】數學不僅是一門學科,也是一種文化,即數學文化.數學文化包括數學史、數學美和數學應用等多方面.古時候,在某個王國里有一位聰明的大臣,他發明了國際象棋,獻給了國王,國王從此迷上了下棋,為了對聰明的大臣表示感謝,國王答應滿足這位大臣的一個要求.大臣說:“就在這個棋盤上放一些米粒吧.第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,然后是
粒米,然后是![]() 粒、
粒、![]() 粒、
粒、![]() 粒······一只到第
粒······一只到第![]() 格.”“你真傻!就要這么一點米粒?”國王哈哈大笑.大臣說:“就怕您的國庫里沒有這么多米!”國王的國庫里真沒有這么多米嗎?題中問題就是求
格.”“你真傻!就要這么一點米粒?”國王哈哈大笑.大臣說:“就怕您的國庫里沒有這么多米!”國王的國庫里真沒有這么多米嗎?題中問題就是求![]() 是多少?請同學們閱讀以下解答過程就知道答案了.
是多少?請同學們閱讀以下解答過程就知道答案了.
設![]() ,
,
則![]()
![]()
![]()
即:![]()
事實上,按照這位大臣的要求,放滿一個棋盤上的![]() 個格子需要
個格子需要![]() 粒米.那么
粒米.那么![]() 到底多大呢?借助計算機中的計算器進行計算,可知答案是一個
到底多大呢?借助計算機中的計算器進行計算,可知答案是一個![]() 位數:
位數:![]()
![]() ,這是一個非常大的數,所以國王是不能滿足大臣的要求.請用你學到的方法解決以下問題:
,這是一個非常大的數,所以國王是不能滿足大臣的要求.請用你學到的方法解決以下問題:
![]() 我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座
我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座![]() 層塔共掛了
層塔共掛了![]() 盞燈,且相鄰兩層中的下一層燈數是上一層燈數的
盞燈,且相鄰兩層中的下一層燈數是上一層燈數的![]() 倍,則塔的頂層共有多少盞燈?
倍,則塔的頂層共有多少盞燈?
![]() 計算:
計算: ![]()
![]() 某中學“數學社團”開發了一款應用軟件,推出了“解數學題獲取軟件激活碼”的活動.這款軟件的激活碼為下面數學問題的答案:
某中學“數學社團”開發了一款應用軟件,推出了“解數學題獲取軟件激活碼”的活動.這款軟件的激活碼為下面數學問題的答案:
已知一列數:![]() ,其中第一項是
,其中第一項是![]() ,接下來的兩項是
,接下來的兩項是![]() ,再接下來的三項是
,再接下來的三項是![]() ,以此類推,求滿足如下條件的所有正整數
,以此類推,求滿足如下條件的所有正整數![]() ,且這一數列前
,且這一數列前![]() 項和為
項和為![]() 的正整數冪.請直接寫出所有滿足條件的軟件激活碼正整數
的正整數冪.請直接寫出所有滿足條件的軟件激活碼正整數![]() 的值.
的值.
【答案】(1)3;(2)![]() ;(3)
;(3)![]()
【解析】
![]() 設塔的頂層共有
設塔的頂層共有![]() 盞燈,根據題意列出方程,進行解答即可.
盞燈,根據題意列出方程,進行解答即可.
![]() 參照題目中的解題方法進行計算即可.
參照題目中的解題方法進行計算即可.
![]() 由題意求得數列的每一項,及前n項和Sn=2n+1-2-n,及項數,由題意可知:2n+1為2的整數冪.只需將-2-n消去即可,分別分別即可求得N的值
由題意求得數列的每一項,及前n項和Sn=2n+1-2-n,及項數,由題意可知:2n+1為2的整數冪.只需將-2-n消去即可,分別分別即可求得N的值
![]() 設塔的頂層共有
設塔的頂層共有![]() 盞燈,由題意得
盞燈,由題意得
![]() .
.
解得![]() ,
,
![]() 頂層共有
頂層共有![]() 盞燈.
盞燈.
![]() 設
設![]() ,
,
![]()
![]() ,
,
即:![]()
![]() .
.
即![]()
![]() 由題意可知:20第一項,20,21第二項,20,21,22第三項,…20,21,22…,2n1第n項,
由題意可知:20第一項,20,21第二項,20,21,22第三項,…20,21,22…,2n1第n項,
根據等比數列前n項和公式,求得每項和分別為:![]()
每項含有的項數為:1,2,3,…,n,
總共的項數為![]()
所有項數的和為![]()
![]()
![]()
![]()
由題意可知:![]() 為2的整數冪,只需將2n消去即可,
為2的整數冪,只需將2n消去即可,
則①1+2+(2n)=0,解得:n=1,總共有![]() ,不滿足N>10,
,不滿足N>10,
②1+2+4+(2n)=0,解得:n=5,總共有![]() 滿足
滿足![]() ,
,
③1+2+4+8+(2n)=0,解得:n=13,總共有![]() 滿足
滿足![]() ,
,
④1+2+4+8+16+(2n)=0,解得:n=29,總共有![]() 不滿足
不滿足![]() ,
,
∴![]()


科目:初中數學 來源: 題型:
【題目】學校準備購進一批A、B兩型號節能燈,已知2只A型節能燈和3只B型節能燈共需31元;1只A型節能燈和2只B型節能燈共需19元.
(1)求一只A型節能燈和一只B型節能燈的售價各是多少元?
(2)學校準備購進這兩種型號的節能燈共100只,并且A型節能燈的數量不多于B型節能燈數量的2倍,請設計出最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品的進價為每件40元,售價為每件50元,每個月可賣出200件.如果每件商品的售價每上漲2元,則每個月少賣5件,設每件商品的售價為x元,則可賣y件,每個月銷售利潤為w元.
(1)求y與x的函數關系式;
(2)每件商品的售價定為多少元時,每個月可獲得最大利潤?最大的月利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
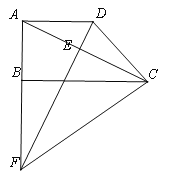
【題目】如圖,已知梯形ABCD中,AD//BC ,∠ABC=90°,BC=2AB=8,對角線AC平分∠BCD,過點D作DE⊥AC,垂足為點E,交邊AB的延長線于點F,聯結CF.
(1)求腰DC的長;
(2)求∠BCF的余弦值.
查看答案和解析>>
科目:初中數學 來源: 題型:
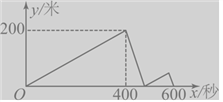
【題目】甲、乙兩人在同一直線噵路上同起點,同方向同進出發,分別以不同的速度勻速跑步1500米,當甲超出乙200米時,甲停下來等候乙,甲、乙會合后,兩人分別以原來的速度繼續跑向終點,先到達終點的人在終點休息,在跑步的整個過程中,甲、乙兩人的距離y(米)與出發的時間x(秒)之間的關系如圖所示,則甲到終點時,乙距離終點______________米。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在△ABC中,AB=AC. (1)若∠A=36,在△ABC中畫一條線段,能得到2個等腰三角形(不包括△ABC),這2個等腰三角形的頂角的度數分別是_____;(2)若∠A≠36, 當∠A=_____時,在等腰△ABC中畫一條線段,能得到2個等腰三角形(不包括△ABC).(寫出兩個答案即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的方程(2m+1)x2+4mx+2m﹣3=0有兩個不相等的實數根.
(1)求m的取值范圍;
(2)是否存在實數m,使方程的兩個實數根的倒數之和等于﹣1?若存在,求出m的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
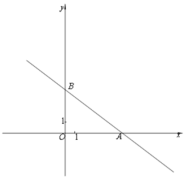
【題目】在平面直角坐標系![]() 中,直線
中,直線![]()
![]() 與
與![]() 軸、
軸、![]() 軸分別交于點A、B如圖所示,點
軸分別交于點A、B如圖所示,點![]() 在線段
在線段![]() 的延長線上,且
的延長線上,且![]() .
.
(1)用含字母![]() 的代數式表示點
的代數式表示點![]() 的坐標;
的坐標;
(2)拋物線y經過點![]() 、
、![]() ,求此拋物線的表達式;
,求此拋物線的表達式;
(3)在第(2)題的條件下,位于第四象限的拋物線上,是否存在這樣的點![]() :使
:使![]() ,如果存在,求出點
,如果存在,求出點![]() 的坐標,如果不存在,試說明理由.
的坐標,如果不存在,試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
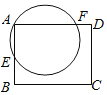
【題目】如圖,在矩形ABCD中,過點A的圓O交邊AB于點E,交邊AD于點F,已知AD=5,AE=2,AF=4.如果以點D為圓心,r為半徑的圓D與圓O有兩個公共點,那么r的取值范圍是______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com