【題目】如圖，一次函數y=kx+3的圖象與反比例函數
的圖象交于P、Q兩點，PA⊥x軸于點A，一次函數的圖象分別交x軸、y軸于點C、點B，其中OA=6，且
.
(1)求一次函數和反比例函數的表達式；
(2)求△APQ的面積；
(3)根據圖象寫出當x取何值時，一次函數的值小于反比例函數的值.
【答案】（1）y=-
x+3，y=-
；（2）S△APQ=30；（3）當-4<x<0或x>6時，一次函數的值小于反比例函數的值．
【解析】
（1）根據題意求得C（2，0）．將C代入y=kx+3中，即可得到一次函數的表達式．
根據題意求得P（6，-6）．將點P（6，-6）代入反比例函數y=
，即可得到反比例函數的表達式．
（2）聯立直線PQ與反比例函數解析式，得到Q點坐標．再根據三角形的面積公式即可得到答案.
（3）通過觀察圖像即可得到答案.
（1）∵OA=6，且
，
∴OA=3OC=6，
∴OC=2，即C（2，0）．
將C（2，0）代入y=kx+3中，
得：0=2k+3，解得：k=-，
∴一次函數的表達式為y=-x+3．
令y=-x+3中x=6，則y=-6，
∴P（6，-6）．
∵點P（6，-6）在反比例函數y=的圖象上，
∴m=6×（-6）=-36，
∴反比例函數的表達式為y=-．
（2）聯立直線PQ與反比例函數解析式，
得：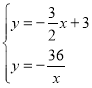
，解得：
，或
，
∴Q（-4，9）．
∴S△APQ=
AC（yQ-yP）=×（6-2）×[9-（-6）]=30．
（3）觀察函數圖象發現：
當-4<x<0或x>6時，一次函數圖象在反比例函數圖象的下方，
∴當-4<x<0或x>6時，一次函數的值小于反比例函數的值．
愉快的寒假南京出版社系列答案科目：初中數學 來源： 題型：
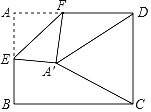
【題目】如圖，在矩形紙片ABCD中，AB＝4，BC＝4
，點E是AB的中點，點F是AD邊上的一個動點，將△AEF沿EF所在直線翻折，得到△A'EF，連接A'C，A'D，則當△A'DC是以A'D為腰的等腰三角形時，FD的長是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某網店專售一款電動牙刷，其成本為20元/支，銷售中發現，該商品每天的銷售量y(支）與銷售單價x(元/支）之間存在如圖所示的關系．
(1)求y與x之間的函數關系式．
(2)由于湖北省武漢市爆發了新型冠狀病毒肺炎（簡稱“新冠肺炎”）疫情，該網店店主決定從每天獲得的利潤中抽出200元捐獻給武漢，為了保證捐款后每天剩余利潤不低于550元，如何確定這款電動牙刷的銷售單價？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】以下說法正確的是( )
A.小明做了
次擲圖釘的實驗，發現
次釘尖朝上，由此他說釘尖朝上的概率是
B.一組對邊平行，另一組對邊相等的四邊形是平行四邊形
C.點
都在反比例函數
圖象上，且
則
；
D.對于一元二元方程
，若
則方程的兩個根互為相反數
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】深圳某百果園店售賣贛南臍橙，已知每千克臍橙的成本價為
元，在銷售臍橙的這
天時間內，銷售單價
（元/千克）與時間第
（天）之間的函數關系式為
（
，且為整數），日銷售量
（千克）與時間第（天）之間的函數關系式為
（，且為整數）
（1）請你直接寫出日銷售利潤
（元）與時間第（天）之間的函數關系式；
（2）該店有多少天日銷售利潤不低于
元？
（3）在實際銷售中，該店決定每銷售
千克臍橙，就捐贈
元給希望工程，在這天中，每天扣除捐贈后的日銷售利潤隨時間的增大而增大，求
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】揭西縣圍繞“推進‘六穩’，拉動消費”為主題，舉辦“揭西人游揭西”活動，從4月份到6月份，分批次免費游覽縣內相關旅游景區景點．某班級全班同學分別從A、B、C、D、E五個景區中選出自己最喜歡的一個，繪制出如下的統計圖①和圖②，請根據相關信息，解答下列問題：
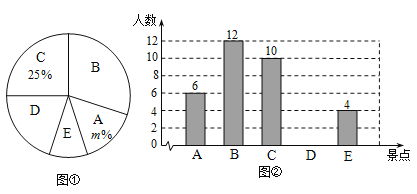
（1）圖①中m的值為．扇形統計圖中，B景區所對的圓心角的大小是；
（2）補全條形統計圖；
（3）甲乙兩個同學分別從A、B、C、D四個景區中隨機挑出一個景區各自游玩，請用樹狀圖或列表的方法求出他們剛好選到同一個景區的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在完善基礎設施、改善市容市貌、提升城市品質過程中，2019年我市開展人行道改造工程，需要花崗巖地板磚鋪設人行道．現租用甲、乙兩種貨車運載地板磚，已知一輛甲車每次運載的重量比一輛乙車多2噸，且甲車運載16噸地板磚和乙車運載12噸地板磚所用的車輛數相同．
（1）甲、乙兩種貨車每次運載地板磚各多少噸？
（2）現租用甲車a輛、乙車b輛，剛好運載地板磚100噸，且a≤3b，共有多少種租車方案？
（3）在（2）中已知一輛甲車每次的運費是380元，一輛乙車每次的運費是300元，如何租用甲、乙兩種車可使得總運費最低？求出最低總運費．
查看答案和解析>>
科目：初中數學 來源： 題型：
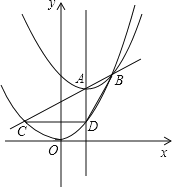
【題目】A是直線x=1上一個動點，以A為頂點的拋物線y1=a(x﹣1)2+t和拋物線y2=ax2交于點B(A，B不重合，a是常數)，直線AB和拋物線y2=ax2交于點B，C，直線x=1和拋物線y2=ax2交于點D．(如圖僅供參考)
(1)求點B的坐標(用含有a，t的式子表示)；
(2)若a＜0，且點A向上移動時，點B也向上移動，求
的范圍；
(3)當B，C重合時，求的值；
(4)當a＞0，且△BCD的面積恰好為3a時，求的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一個批發商銷售成本為20元/千克的某產品，根據物價部門規定：該產品每千克售價不得超過90元，在銷售過程中發現的售量y（千克）與售價x（元/千克）滿足一次函數關系，對應關系如下表：
售價x（元/千克） | … | 50 | 60 | 70 | 80 | … |
銷售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y與x的函數關系式；
（2）該批發商若想獲得4000元的利潤，應將售價定為多少元？
（3）該產品每千克售價為多少元時，批發商獲得的利潤w（元）最大？此時的最大利潤為多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com