
【題目】對于兩個不相等的實數a,b,我們規定符號max{a,b}表示a、b中的較大的數,如:max{2,4}=4,按照這個規定,方程max{x,﹣x}=x2﹣x﹣1的解為( )
A.1+![]() 或1﹣
或1﹣![]() B.1或﹣1C.1﹣
B.1或﹣1C.1﹣![]() 或1D.1+
或1D.1+![]() 或﹣1
或﹣1
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
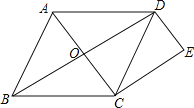
【題目】如圖,點O是菱形ABCD對角線的交點,過點C作CE∥OD,過點D作DE∥AC,CE與DE相交于點E.
(1)求證:四邊形OCED是矩形.
(2)若AB=4,∠ABC=60°,求矩形OCED的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀對話,解答問題:

(1)分別用a、b表示小冬從小麗、小兵袋子中抽出的卡片上標有的數字,請用樹狀圖法或列表法寫出(a,b)的所有取值;
(2)求在(a,b)中使關于x的一元二次方程x2﹣ax+2b=0有實數根的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y=2x+b與雙曲線![]() 交于A,B兩點.P是線段AB上一點(不與點A,點B重合),過點P作平行于x軸的直線交雙曲線
交于A,B兩點.P是線段AB上一點(不與點A,點B重合),過點P作平行于x軸的直線交雙曲線![]() 于點M,過點P作平行于y軸的直線交雙曲線
于點M,過點P作平行于y軸的直線交雙曲線![]() 于點N.
于點N.
(1)當點A的橫坐標為1時,求b的值:
(2)在(1)的條件下,設P點的橫坐標為m,
①若m=-1,判斷PM與PN的數量關系,并說明理由;
②若PM<PN,結合函數圖象,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,我們把以拋物線![]() 上的動點A為頂點的拋物線叫做這條拋物線的“子拋物線”.如圖,已知某條“子拋物線”的二次項系數為
上的動點A為頂點的拋物線叫做這條拋物線的“子拋物線”.如圖,已知某條“子拋物線”的二次項系數為![]() ,且與y軸交于點C.設點A的橫坐標為m(m>0),過點A作y軸的垂線交y軸于點B.
,且與y軸交于點C.設點A的橫坐標為m(m>0),過點A作y軸的垂線交y軸于點B.
(1)當m=1時,求這條“子拋物線”的解析式;
(2)用含m的代數式表示∠ACB的余切值;
(3)如果∠OAC=135°,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家所在居民樓的對面有一座大廈AB,高為74米,為測量居民樓與大廈之間的距離,小明從自己家的窗戶C處測得大廈頂部A的仰角為37°,大廈底部B的俯角為48°.
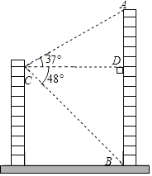
(1)求∠ACB的度數;
(2)求小明家所在居民樓與大廈之間的距離.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
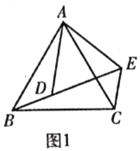
【題目】(1)(問題發現)如圖1,![]() 和
和![]() 均為等邊三角形,點
均為等邊三角形,點![]() ,
,![]() ,
,![]() 在同一條直線上.填空:①線段
在同一條直線上.填空:①線段![]() ,
,![]() 之間的數量關系為______;②
之間的數量關系為______;②![]() _____°.
_____°.
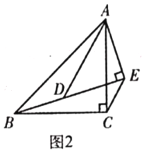
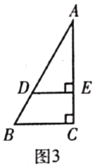
(2)(類比探究)如圖2,![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,
,![]() ,
,![]() ,點
,點![]() ,
,![]() ,
,![]() 在同一條直線上,請判斷線段
在同一條直線上,請判斷線段![]() ,
,![]() 之間的數量關系及
之間的數量關系及![]() 的度數,并給出證明.
的度數,并給出證明.
(3)(解決問題)如圖3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 邊上,
邊上,![]() 于點
于點![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 旋轉,當
旋轉,當![]() 所在直線經過點
所在直線經過點![]() 時,
時,![]() 的長是多少?(直接寫出答案)
的長是多少?(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
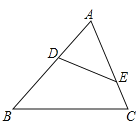
【題目】如圖,在△ABC中,點D、E分別在邊AB、AC上,則在下列五個條件中:①∠AED=∠B;②DE∥BC;③![]() =
=![]() ;④AD·BC=DE·AC;⑤∠ADE=∠C,能滿足△ADE∽△ACB的條件有( )
;④AD·BC=DE·AC;⑤∠ADE=∠C,能滿足△ADE∽△ACB的條件有( )
A.1個B.2C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() ,直線
,直線![]() 與雙曲線
與雙曲線![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .探究:由雙曲線
.探究:由雙曲線![]() 與線段
與線段![]() 圍成的區域
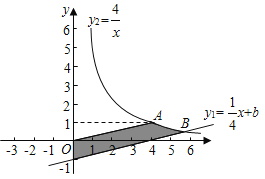
圍成的區域![]() 內(不含邊界)整點的個數(點的橫、縱坐標都是整數的點稱為整點).①當
內(不含邊界)整點的個數(點的橫、縱坐標都是整數的點稱為整點).①當![]() 時,如圖,區域
時,如圖,區域![]() 內的整點的個數為_____;②若區域
內的整點的個數為_____;②若區域![]() 內恰有4個整點,結合函數圖象,則
內恰有4個整點,結合函數圖象,則![]() 的取值范圍是_______
的取值范圍是_______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com