
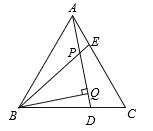
【題目】已知:如圖,△ABC是等邊三角形,AE=CD,BQ⊥AD于Q,BE交AD于點(diǎn)P.
(1)求證:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
【答案】(1)見(jiàn)解析;(2)PE=1.
【解析】
(1)根據(jù)等邊三角形的性質(zhì)得到AB=AC,∠BAE=∠C=60°,證明△ABE≌△CAD
(2)根據(jù)直角三角形的性質(zhì)得到BP=2PQ,再根據(jù)題意BP=2PQ =4,則PE =1.
(1)∵△ABC是等邊三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,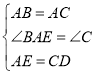 ,
,
∴△ABE≌△CAD(SAS),
(2) ∵△ABE≌△CAD,
∴∠ABE=∠CAQ,
∴∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=∠BAC=60°,∵BQ⊥AD,
∴∠PBQ=90°∠BPQ=90°60°=30°,
∴BP=2PQ.
∵PQ=2,BE=5,
則BP=2PQ =4,PE = BE- PB=5-4=1.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在數(shù)軸上點(diǎn)A表示-3,點(diǎn)B表示4.
(1)點(diǎn)A與點(diǎn)B之間的距離是 ;
(2)我們知道,在數(shù)軸上|a|表示數(shù)a所對(duì)應(yīng)的點(diǎn)到原點(diǎn)的距離,你能說(shuō)明![]() 在數(shù)軸上表示的意義嗎?
在數(shù)軸上表示的意義嗎?
(3)在數(shù)軸上點(diǎn)P表示的數(shù)為x,是否存在這樣的點(diǎn)P,使2PA+PB=12?若存在,請(qǐng)求出相應(yīng)的x;若不存在,請(qǐng)說(shuō)明理由.
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】數(shù)學(xué)活動(dòng)
問(wèn)題情境:
如圖1,在ABC中,AB=AC,∠BAC=90°,D,E分別是邊AB,AC的中點(diǎn),將ADE繞點(diǎn)A順時(shí)針旋轉(zhuǎn)α角(0°<α<90°)得到AD′E′,連接CE′,BD′.探究CE′與BD′的數(shù)量關(guān)系;
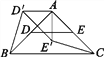 圖1
圖1 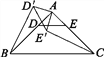 圖2
圖2 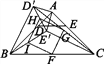 圖3
圖3 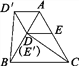 圖4
圖4
探究發(fā)現(xiàn):
(1)圖1中,CE′與BD′的數(shù)量關(guān)系是________;
(2)如圖2,若將問(wèn)題中的條件“D,E分別是邊AB,AC的中點(diǎn)”改為“D為AB邊上任意一點(diǎn),DE∥BC交AC于點(diǎn)E”,其他條件不變,(1)中CE′與BD′的數(shù)量關(guān)系還成立嗎?請(qǐng)說(shuō)明理由;
拓展延伸:
(3)如圖3,在(2)的條件下,連接BE′,CD′,分別取BC,CD′,E′D′,BE′的中點(diǎn)F,G,H,I,順次連接F,G,H,I得到四邊形FGHI.請(qǐng)判斷四邊形FGHI的形狀,并說(shuō)明理由;
(4)如圖4,在ABC中,AB=AC,∠BAC=60°,點(diǎn)D,E分別在AB,AC上,且DE∥BC,將ADE繞點(diǎn)A順時(shí)針旋轉(zhuǎn)60°得到AD′E′,連接CE′,BD′.請(qǐng)你仔細(xì)觀察,提出一個(gè)你最關(guān)心的數(shù)學(xué)問(wèn)題(例如:CE′與BD′相等嗎?).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
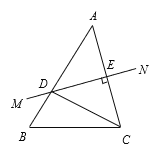
【題目】如圖,在△ABC中,AC的垂直平分線MN分別交AB,AC于D,E.若AE=5,△BCD的周長(zhǎng)17,求△ABC的周長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,AC的垂直平分線MN分別交AB,AC于D,E.若AE=5,△BCD的周長(zhǎng)17,求△ABC的周長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)如圖1,在△ABC中,∠ACB=90°,AC=BC,直線l過(guò)點(diǎn)C,點(diǎn)A,B在直線l同側(cè),BD⊥l,AE⊥l,垂足分別為D,E.求證:△AEC≌△CDB.
(2)如圖2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的結(jié)論,請(qǐng)按照?qǐng)D中所標(biāo)注的數(shù)據(jù)計(jì)算圖中實(shí)線所圍成的圖形的面積S= .

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】近期電影《少年的你》受到廣大青少年的喜愛(ài),某校七年級(jí)1班2班的幾名同學(xué)請(qǐng)他們的家長(zhǎng)在網(wǎng)上買(mǎi)票,家長(zhǎng)了解到某電影院的活動(dòng),設(shè)購(gòu)買(mǎi)電影票的張數(shù)為![]()
購(gòu)買(mǎi)張數(shù) |
|
|
|
每張票的價(jià)格 |
|
|
|
家長(zhǎng)溝通后決定兩個(gè)班的同學(xué)在期中考試結(jié)束后去觀看。兩個(gè)班共有![]() 人,期中
人,期中![]() 班人數(shù)多于
班人數(shù)多于![]() 不足
不足![]() 人。經(jīng)過(guò)估算,如果兩個(gè)班都以班為單位購(gòu)買(mǎi),則一共應(yīng)付
人。經(jīng)過(guò)估算,如果兩個(gè)班都以班為單位購(gòu)買(mǎi),則一共應(yīng)付![]() 元。
元。
![]() 求兩個(gè)班有多少個(gè)同學(xué)?
求兩個(gè)班有多少個(gè)同學(xué)?
![]() 如果兩個(gè)班聯(lián)合起來(lái),作為一個(gè)團(tuán)體購(gòu)票,可以節(jié)省多少錢(qián)?
如果兩個(gè)班聯(lián)合起來(lái),作為一個(gè)團(tuán)體購(gòu)票,可以節(jié)省多少錢(qián)?
![]() 如果七年級(jí)
如果七年級(jí)![]() 班同學(xué)作為一個(gè)團(tuán)體購(gòu)票,你認(rèn)為如何購(gòu)票才最省錢(qián)?可以節(jié)省多少錢(qián)?
班同學(xué)作為一個(gè)團(tuán)體購(gòu)票,你認(rèn)為如何購(gòu)票才最省錢(qián)?可以節(jié)省多少錢(qián)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
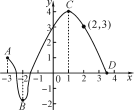
【題目】已知兩個(gè)變量x,y之間的變化情況如圖所示,根據(jù)圖象回答下列問(wèn)題:
(1)寫(xiě)出y的變化范圍;
(2)求當(dāng)x=0,-3時(shí),y的對(duì)應(yīng)值;
(3)求當(dāng)y=0,3時(shí),對(duì)應(yīng)的x的值;
(4)當(dāng)x為何值時(shí),y的值最大?
(5)當(dāng)x在什么范圍內(nèi)時(shí),y的值在不斷增加?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com