
【題目】采用東陽南棗通過古法熬制而成的蜜棗是我們東陽的土特產之一,已知蜜棗每袋成本10元.試銷后發現每袋的銷售價![]() (元)與日銷售量
(元)與日銷售量![]() (袋)之間的關系如下表:
(袋)之間的關系如下表:
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
若日銷售量![]() 是銷售價
是銷售價![]() 的一次函數,試求:
的一次函數,試求:
(1)日銷售量![]() (袋)與銷售價
(袋)與銷售價![]() (元)的函數關系式.
(元)的函數關系式.
(2)要使這種蜜棗每日銷售的利潤最大,每袋的銷售價應定為多少元?每日銷售的最大利潤是多少元?
【答案】(1) ![]() ;(2) 要使這種蜜棗每日銷售的利潤最大,每袋的銷售價應定為25元,每日銷售的最大利潤是225元.
;(2) 要使這種蜜棗每日銷售的利潤最大,每袋的銷售價應定為25元,每日銷售的最大利潤是225元.
【解析】
(1)根據表格中的數據,利用待定系數法,求出日銷售量y(袋)與銷售價x(元)的函數關系式即可
(2)利用每件利潤×總銷量=總利潤,進而求出二次函數最值即可.
(1)依題意,根據表格的數據,設日銷售量y(袋)與銷售價x(元)的函數關系式為y=kx+b得![]() ,解得
,解得![]()
故日銷售量y(袋)與銷售價x(元)的函數關系式為:y=x+40
(2)設利潤為![]() 元,得
元,得
![]()
![]()
![]()
∵![]()
∴當![]() 時,
時,![]() 取得最大值,最大值為225
取得最大值,最大值為225
故要使這種蜜棗每日銷售的利潤最大,每袋的銷售價應定為25元,每日銷售的最大利潤是225元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
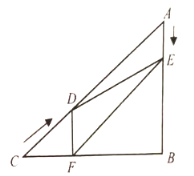
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發,沿
出發,沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() ;同時,動點
;同時,動點![]() 從點
從點![]() 出發,沿
出發,沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() ;當一個點停止運動,另一個點也停止運動.設點
;當一個點停止運動,另一個點也停止運動.設點![]() ,
,![]() 運動的時間是
運動的時間是![]()
![]()
![]() .過點
.過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)![]() 為何值時,
為何值時,![]() ?
?
(2)設四邊形![]() 的面積為
的面積為![]() ,試求出
,試求出![]() 與
與![]() 之間的關系式;
之間的關系式;
(3)是否存在某一時刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(4)當![]() 為何值時,
為何值時,![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
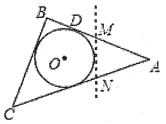
【題目】如圖,△ABC是一張周長為18cm的三角形紙片,BC=5cm,⊙O是它的內切圓,小明用剪刀在⊙O的右側沿著與⊙O相切的任意一條直線![]() 剪下△AMN,則剪下的三角形的周長為( )
剪下△AMN,則剪下的三角形的周長為( )
A.![]() B.
B.![]() C.
C.![]() D.隨直線
D.隨直線![]() 的變化而變化
的變化而變化
查看答案和解析>>
科目:初中數學 來源: 題型:
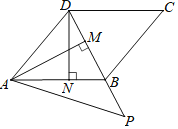
【題目】如圖,在平行四邊形ABCD中,連接BD,且BD=CD,過點A作AM⊥BD于點M,過點D作DN⊥AB于點N,DN=3![]() ,在DB的延長線上取一點P,滿足∠ABD=∠MAP+∠PAB,則AP=( )
,在DB的延長線上取一點P,滿足∠ABD=∠MAP+∠PAB,則AP=( )
A.4.5B.5.5C.6D.6.5
查看答案和解析>>
科目:初中數學 來源: 題型:
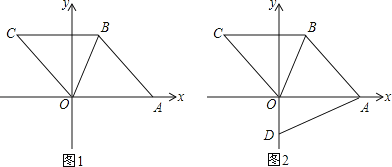
【題目】平面直角坐標系中,四邊形ABCO是菱形,點C的坐標為(﹣3,4),點A在x軸的正半軸上,O為坐標原點,連接OB,拋物線y=ax2+bx+c經過C、O、A三點.
(1)直接寫出這條拋物線的解析式;
(2)如圖1,對于所求拋物線對稱軸上的一點E,設△EBO的面積為S1,菱形ABCO的面積為S2,當S1≤![]() S2時,求點E的縱坐標n的取值范圍;
S2時,求點E的縱坐標n的取值范圍;
(3)如圖2,D(0,﹣![]() )為y軸上一點,連接AD,動點P從點O出發,以
)為y軸上一點,連接AD,動點P從點O出發,以![]() 個單位/秒的速度沿OB方向運動,1秒后,動點Q從O出發,以2個單位/秒的速度沿折線O﹣A﹣B方向運動,設點P運動時間為t秒(0<t≤6),是否存在實數t,使得以P、Q、B為頂點的三角形與△ADO相似?若存在,求出相應的t值;若不存在,請說明理由.
個單位/秒的速度沿OB方向運動,1秒后,動點Q從O出發,以2個單位/秒的速度沿折線O﹣A﹣B方向運動,設點P運動時間為t秒(0<t≤6),是否存在實數t,使得以P、Q、B為頂點的三角形與△ADO相似?若存在,求出相應的t值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】省射擊隊為從甲、乙兩名運動員中選拔一人參加全國比賽,對他們進行了六次測試,測試成績如下表(單位:環):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 10 | 10 | 9 | 8 |
(1)根據表格中的數據,可計算出甲的平均成績是 環(直接寫出結果);
(2)已知乙的平均成績是9環,試計算其第二次測試成績的環數;
(3)分別計算甲、乙六次測試成績的方差,根據計算的結果,你認為推薦誰參加全國比賽更合適,請說明理由.
(計算方差的公式:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,從一塊圓形紙片上剪出一個圓心角為90°的扇形ABC,使點A、B、C在圓周上,將剪下的扇形作為一個圓錐側面,如果圓錐的高為![]() ,則這塊圓形紙片的直徑為( )
,則這塊圓形紙片的直徑為( )
A. 12cm B. 20cm C. 24cm D. 28cm
查看答案和解析>>
科目:初中數學 來源: 題型:
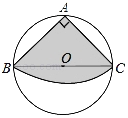
【題目】(1)(學習心得)于彤同學在學習完“圓”這一章內容后,感覺到一些幾何問題如果添加輔助圓,運用圓的知識解決,可以使問題變得非常容易.例如:如圖1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 外一點,且
外一點,且![]() ,求
,求![]() 的度數.若以點
的度數.若以點![]() 為圓心,
為圓心,![]() 為半徑作輔助
為半徑作輔助![]() ,則
,則![]() 、
、![]() 必在
必在![]() 上,
上,![]() 是
是![]() 的圓心角,而
的圓心角,而![]() 是圓周角,從而可容易得到
是圓周角,從而可容易得到![]() =________
=________![]() .
.
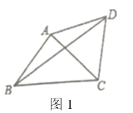
(2)(問題解決)如圖2,在四邊形![]() 中,
中,![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
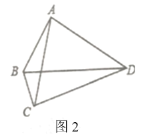
(3)(問題拓展)如圖3,![]() 是正方形
是正方形![]() 的邊
的邊![]() 上兩個動點,滿足
上兩個動點,滿足![]() .連接交于點,連接
.連接交于點,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() 交于點
交于點![]() ,若正方形的邊長為2,則線段
,若正方形的邊長為2,則線段![]() 長度的最小值是_______.
長度的最小值是_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com