【題目】已知∠AED=∠C,∠1+∠2=180°.請說明∠BEC=∠FGC
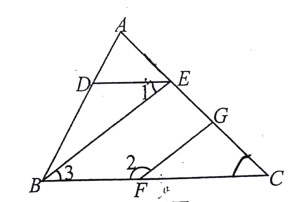
解：因為∠AED=∠C(已知)，
所以________∥_______（_________________________________ ）
得∠1=∠3（ _______________________________ ）
又∠1+∠2=180°（已知），
得∠3+∠2=180°（___________________________）
所以_______∥_______
所以∠BEC=∠FGC（___________________________）
藍天教育暑假優化學習系列答案科目：初中數學 來源： 題型：
【題目】下表是某校七～九年級某月課外興趣小組活動時間統計表，其中各年級同一興趣小組每次活動時間相同，文藝小組每次活動時間比科技小組每次活動時間多0.5小時.設文藝小組每次活動時間為
小時，請根據表中信息完成下列解答.
課外小組活動 總時間（小時） | 文藝小組 活動次數 | 科技小組 活動次數 | |
七年級 | 12.5 | 4 | 3 |
八年級 | 10.5 | 3 |
|
九年級 | 7 |
|
|
（1）科技小組每次活動時間為______小時（用含的式子表示）；
（2）求八年級科技小組活動次數
的值；
（3）直接寫出
______，
______.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如下數表是由從1 開始的連續自然數組成，觀察規律并完成各題的解答.
（1）表中第8行的最后一個數是_____，它是自然數_____的平方，第8行共有 _____個數；
（2）用含n的代數式表示：第n行的第一個數是_____，最后一個數是_____，第n行共有_____個數；
（3）求第n行各數之和．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】立定跳遠是體育中考選考項目之一，體育課上老師記錄了某同學的一組立定跳遠成績如表：
成績（m） | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
則下列關于這組數據的說法，正確的是（ ）
A.眾數是2.3B.平均數是2.4
C.中位數是2.5D.方差是0.01
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,直線AB∥CD,點E在直線AB上,點G在直線CD上,點P在直線AB.CD之間,∠AEP=40°,∠EPG=900
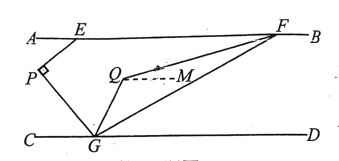
(1)填空:∠PGC=_________0；
(2)如圖, 點F在直線AB上,聯結FG,∠EFG的平分線與∠PGD的平分線相交于點Q，當點F在點E的右側時,如果∠EFG=30°,求∠FQG的度數；
解:過點Q作QM∥CD
因為∠PGC+∠PGD=1800
由(1)得∠PGC=_______0,
所以∠PGD=1800-∠PGC=________0,
因為GQ平分∠PGD,
所以∠PGQ=∠QGD=
∠PGD=_________0
(下面請補充完整求∠FQG度數的解題過程)
(3)點F在直線AB上,聯結FG,∠EFG的平分線與∠PGD的平分線相交于點Q.如果∠FQG=2∠BFG,請直接寫出∠EFG的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，將一張矩形紙ABCD沿著對角線BD向上折疊，頂點C落到點E處，BE交AD于點F．
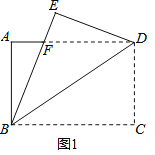
（1）求證：
是等腰三角形；
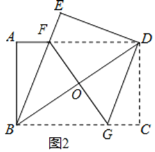
（2）如圖2，過點D作
，交BC于點G，連接FG交BD于點O．
①試判斷四邊形BGDF的形狀，并說明理由；
②若
，
，求FG的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】問題再現：
數形結合是一種重要的數學思想方法，借助這種思想方法可將抽象的數學知識變得直觀并且具有可操作性.初中數學里的一些代數公式，很多都可以通過表示幾何圖形面積的方法進行直觀推導和解釋.
例如：利用圖形的幾何意義驗證完全平方公式.
將一個邊長為
的正方形的邊長增加
，形成兩個長方形和兩個正方形，如圖所示：這個圖形的面積可以表示成：
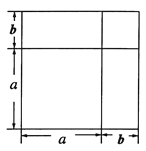
或
∴
這就驗證了兩數和的完全平方公式.
類比解決：
請你類比上述方法，利用圖形的幾何意義驗證平方差公式.
（要求畫出圖形并寫出推理過程）
問題提出：如何利用圖形幾何意義的方法證明
？
如圖所示，
表示1個1×1的正方形，即：
，
表示1個2×2的正方形，
與
恰好可以拼成1個2×2的正方形，因此：、、就可以表示2個2×2的正方形，即：
而、、、恰好可以拼成一個
的大正方形.
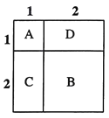
由此可得：
.
嘗試解決：
請你類比上述推導過程，利用圖形的幾何意義確定：
_______.（要求寫出結論并構造圖形寫出推證過程）.
問題拓廣：
請用上面的表示幾何圖形面積的方法探究：
_______.（直接寫出結論即可，不必寫出解題過程）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
