
【題目】如圖,拋物線![]() 與直線
與直線![]() 交于點
交于點![]() ,點
,點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
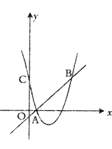
(1)求![]() 的值和拋物線的解析式;
的值和拋物線的解析式;
(2)直接寫出方程![]() 的解;
的解;
(3)點![]() 是拋物線
是拋物線![]() 對稱軸上的一個動點,當(dāng)
對稱軸上的一個動點,當(dāng)![]() 的值最小時,判斷
的值最小時,判斷![]() 的形狀.
的形狀.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 是直角三角形.
是直角三角形.
【解析】
(1)將點A代入直線解析式可求出m,將點A,B代入拋物線解析式可求出b,c,進而得到拋物線的解析式;
(2)根據(jù)拋物線與直線的交點坐標可得所求方程的解;
(3)根據(jù)點B,C關(guān)于對稱軸對稱可知點![]() 是直線
是直線![]() 與拋物線對稱軸的交點時,
與拋物線對稱軸的交點時,![]() 的值最小,依此求出N點坐標,然后設(shè)直線
的值最小,依此求出N點坐標,然后設(shè)直線![]() 交
交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,連結(jié)CN,求出
,連結(jié)CN,求出![]() ,即可得到
,即可得到![]() ,易得
,易得![]() 是直角三角形.
是直角三角形.
解:(1)∵點![]() 在直線
在直線![]() 上,
上,
∴![]() ,解得:
,解得:![]() ,
,
∵拋物線![]() 過點
過點![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)∵拋物線![]() 與直線
與直線![]() 交于點
交于點![]() ,點
,點![]() ,
,
∴方程![]() 的解為:
的解為:![]() ,
,![]() ;
;
(3)由拋物線知,當(dāng)![]() 時,
時,![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,
,
∵![]() ,
,
∴拋物線的對稱軸為![]() ,
,
由點![]() 在拋物線上知,這兩點關(guān)于對稱軸對稱,
在拋物線上知,這兩點關(guān)于對稱軸對稱,
因此,當(dāng)點![]() 是直線
是直線![]() 與拋物線對稱軸的交點時,
與拋物線對稱軸的交點時,![]() 的值最小,
的值最小,
把![]() 代入
代入![]() 得
得![]() ,
,
∴點N的坐標為![]() ,
,
設(shè)直線![]() 交
交![]() 軸于點
軸于點![]() ,則點
,則點![]() 的坐標為
的坐標為![]() ,
,
過點![]() 作
作![]() 于點
于點![]() ,連結(jié)CN,則點
,連結(jié)CN,則點![]() 的坐標為
的坐標為![]() ,
,
于是![]() ,
,
∵![]()
∴![]() ,
,
∴![]()
∴![]() 是直角三角形.
是直角三角形.


科目:初中數(shù)學(xué) 來源: 題型:
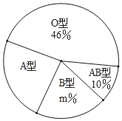
【題目】“只要人人獻出一點愛,世界將變成美好的人間”.某大學(xué)利用“世界獻血日”開展自愿義務(wù)獻血活動,經(jīng)過檢測,獻血者血型有“A、B、AB、O”四種類型,隨機抽取部分獻血結(jié)果進行統(tǒng)計,根據(jù)結(jié)果制作了如圖兩幅不完整統(tǒng)計圖表(表,圖):
血型統(tǒng)計表
血型 | A | B | AB | O |
人數(shù) |
| 10 | 5 |
|
(1)本次隨機抽取獻血者人數(shù)為 人,圖中m= ;
(2)補全表中的數(shù)據(jù);
(3)若這次活動中該校有1300人義務(wù)獻血,估計大約有多少人是A型血?
(4)現(xiàn)有4個自愿獻血者,2人為O型,1人為A型,1人為B型,若在4人中隨機挑選2人,利用樹狀圖或列表法求兩人血型均為O型的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,E,F分別是DC和CB的延長線上的點,且BF=DE,連接AE,AF,EF.

(1)判斷△ABF與△ADE有怎樣的關(guān)系,并說明理由;
(2)求∠EAF的度數(shù),寫出△ABF可以由△ADE經(jīng)過怎樣的圖形變換得到;
(3)若BC=6,DE=2,求△AEF的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
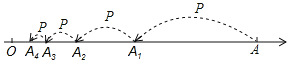
【題目】數(shù)軸上OA兩點的距離為4,一動點P從A點出發(fā)按以下規(guī)律跳動:第一次跳動到AO的中點A1處,第二次從A1點跳動到A1O的中點A2處,第三次從A2跳動到A2O的中點A3處按照這樣的規(guī)律,繼續(xù)跳動到點A4A5A6……An(n≥3,n是整數(shù))處那么線段A3O的長度為_________,AnA的長度為_________ 。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】商店只有雪碧、可樂、果汁、奶汁四種飲料,每種飲料數(shù)量充足,某同學(xué)去該店購買飲料,每種飲料被選中的可能性相同.
(1)若他去買一瓶飲料,則他買到奶汁的概率是 ;
(2)若他兩次去買飲料,每次買一瓶,且兩次所買飲料品種不同,請用樹狀圖或列表法求出他恰好買到雪碧和奶汁的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
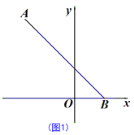
【題目】已知:在平面直角坐標系中,O為坐標原點,A(-5,8),B(3,0).
(1)如圖1,求∠ABO的度數(shù);
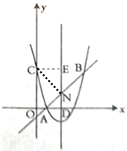
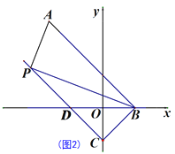
(2)如圖2,點C在y軸的負半軸上,△BOC的面積為![]() ,過點C作CD∥AB交x軸于點D,點P為直線CD上一點,求△PAB的面積;
,過點C作CD∥AB交x軸于點D,點P為直線CD上一點,求△PAB的面積;
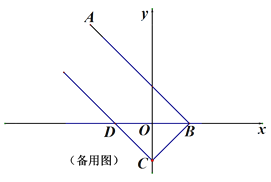
(3)如圖3,在(2)的條件下,當(dāng)P在第二象限時,過點P作AB的垂線交x軸于點E,點F為x軸上一點,連接PF,點G為EP延長線上一點,連接OG,若OG=FP,∠EFP+∠PGO=45°,EF=11,求點P的坐標.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
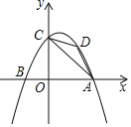
【題目】如圖,二次函數(shù)y=﹣x2+x+2交x軸于點A.B(A在B的右側(cè)),與y軸交于點C,D為第一象限拋物線上的動點,則△ACD面積的最大值是_____
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c與直線y=x交于(1,1)和(3,3)兩點,現(xiàn)有以下結(jié)論:①b2﹣4c>0;②3b+c+6=0;③當(dāng)x2+bx+c>![]() 時,x>2;④當(dāng)1<x<3時,x2+(b﹣1)x+c<0,其中正確的序號是( )
時,x>2;④當(dāng)1<x<3時,x2+(b﹣1)x+c<0,其中正確的序號是( )
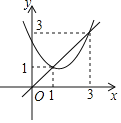
A. ①②④B. ②③④C. ②④D. ③④
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com