
【題目】如圖,已知一次函數(shù)y=kx+b的圖象與x軸,y軸分別相交于A,B兩點(diǎn),且與反比例函數(shù)y=![]() 交于點(diǎn)C,D.作CE⊥x軸,垂足為E,CF⊥y軸,垂足為F.點(diǎn)B為OF的中點(diǎn),四邊形OECF的面積為16,點(diǎn)D的坐標(biāo)為(4,﹣b).
交于點(diǎn)C,D.作CE⊥x軸,垂足為E,CF⊥y軸,垂足為F.點(diǎn)B為OF的中點(diǎn),四邊形OECF的面積為16,點(diǎn)D的坐標(biāo)為(4,﹣b).
(1)求一次函數(shù)表達(dá)式和反比例函數(shù)表達(dá)式;
(2)求出點(diǎn)C坐標(biāo),并根據(jù)圖象直接寫出不等式kx+b≤![]() 的解集.
的解集.
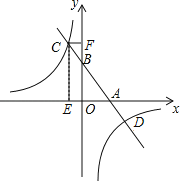
【答案】(1)y=﹣2x+4;(2)﹣2≤x<0或x≥4.
【解析】
(1)由矩形的面積求得m=﹣16,得到反比例函數(shù)的解析式,把D(4,﹣b)代入求得的解析式得到D(4,﹣4),求得b=4,把D(4,﹣4)代入y=kx+4,即可求得一次函數(shù)的解析式;
(2)由一次函數(shù)的解析式求得B的坐標(biāo)為(0,4),根據(jù)題意OF=8,C點(diǎn)的縱坐標(biāo)為8,代入反比例函數(shù)的解析式求得橫坐標(biāo),得到C的坐標(biāo),根據(jù)C、D的坐標(biāo)結(jié)合圖象即可求得不等式kx+b≤![]() 的解集.
的解集.
解:(1)∵CE⊥x軸,CF⊥y軸,
∵四邊形OECF的面積為16,
∴|m|=16,
∵雙曲線位于二、四象限,
∴m=﹣16,
∴反比例函數(shù)表達(dá)式為y=![]() ,
,
將x=4代入y=![]() 得:y=﹣4,
得:y=﹣4,
∴D(4,﹣4),
∴b=4
將D(4,﹣4)代入y=kx+4,得k=﹣2
∴一次函數(shù)的表達(dá)式為y=﹣2x+4;
(2)∵y=﹣2x+4,
∴B(0,4),
∴OF=8,
將y=8代入y=﹣2x+4得x=﹣2,
∴C(﹣2,8),
∴不等式kx+b≤![]() 的解集為﹣2≤x<0或x≥4.
的解集為﹣2≤x<0或x≥4.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() 為一條對(duì)角線,
為一條對(duì)角線,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() .
.
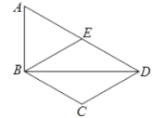
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)連接![]() ,若
,若![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在國(guó)家大數(shù)據(jù)戰(zhàn)略的引領(lǐng)下,我國(guó)在人工智能領(lǐng)域取得顯著成就,自主研發(fā)的人工智能“絕藝”獲得全球最前沿的人工智能賽事冠軍,這得益于所建立的大數(shù)據(jù)中心的規(guī)模和數(shù)據(jù)存儲(chǔ)量,它們決定著人工智能深度學(xué)習(xí)的質(zhì)量和速度,其中的一個(gè)大數(shù)據(jù)中心能存儲(chǔ)580億本書籍,將580億用科學(xué)記數(shù)法表示應(yīng)為( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,菱形ABCD的頂點(diǎn)A在x軸的正半軸上,∠C=60°,頂點(diǎn)B,D的縱坐標(biāo)相同,已知點(diǎn)B的橫坐標(biāo)為7![]() ,若過(guò)點(diǎn)D的雙曲線y=
,若過(guò)點(diǎn)D的雙曲線y=![]() (k>0)恰好過(guò)邊AB的中點(diǎn)E,則k=_____.
(k>0)恰好過(guò)邊AB的中點(diǎn)E,則k=_____.
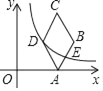
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,已知拋物線![]() 與拋物線
與拋物線![]() 的形狀相同,開(kāi)口方向相反,且相交于點(diǎn)
的形狀相同,開(kāi)口方向相反,且相交于點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() .拋物線
.拋物線![]() 與
與![]() 軸正半軸交于點(diǎn)
軸正半軸交于點(diǎn)![]() 為拋物線
為拋物線![]() 上
上![]() 兩點(diǎn)間一動(dòng)點(diǎn),過(guò)點(diǎn)
兩點(diǎn)間一動(dòng)點(diǎn),過(guò)點(diǎn)![]() 作直線
作直線![]() 軸,與
軸,與![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
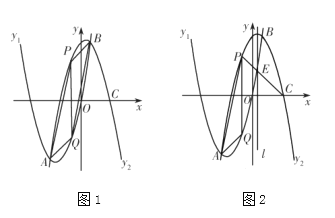
(1)求拋物線![]() 與拋物線
與拋物線![]() 的解析式;
的解析式;
(2)四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值,并寫出此時(shí)點(diǎn)
的最大值,并寫出此時(shí)點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)如圖2,![]() 的對(duì)稱軸為直線
的對(duì)稱軸為直線![]() ,
,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,在(2)的條件下,直線
,在(2)的條件下,直線![]() 上是否存在一點(diǎn)
上是否存在一點(diǎn)![]() ,使得以
,使得以![]() 為頂點(diǎn)的三角形與
為頂點(diǎn)的三角形與![]() 相似?如果存在,求出點(diǎn)
相似?如果存在,求出點(diǎn)![]() 的坐標(biāo);如果不存在,說(shuō)明理由.
的坐標(biāo);如果不存在,說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某興趣小組為了解我市氣溫變化情況,記錄了今年月份連續(xù)![]() 天的最低氣溫(單位:℃):
天的最低氣溫(單位:℃):![]() .關(guān)于這組數(shù)據(jù),下列結(jié)論不正確的是( )
.關(guān)于這組數(shù)據(jù),下列結(jié)論不正確的是( )
A.平均數(shù)是![]() B.中位數(shù)是
B.中位數(shù)是![]() C.眾數(shù)是
C.眾數(shù)是![]() D.方差是
D.方差是![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線![]() 經(jīng)過(guò)點(diǎn)B(3,0),C(0,-2),直線L:
經(jīng)過(guò)點(diǎn)B(3,0),C(0,-2),直線L:![]() 交y軸于點(diǎn)E,且與拋物線交于A,D兩點(diǎn),P為拋物線上一動(dòng)點(diǎn)(不與A重合).
交y軸于點(diǎn)E,且與拋物線交于A,D兩點(diǎn),P為拋物線上一動(dòng)點(diǎn)(不與A重合).
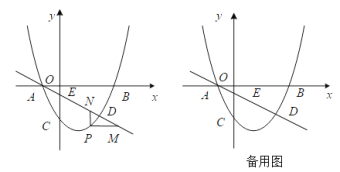
(1)求拋物線的解析式.
(2)當(dāng)點(diǎn)P在直線L下方時(shí),過(guò)點(diǎn)P作PM∥x軸交L于點(diǎn)M,PN∥y軸交L于點(diǎn)N,求PM+PN的最大值.
(3)設(shè)F為直線L上的點(diǎn),以E,C,P,F為頂點(diǎn)的四邊形能否構(gòu)成平行四邊形?若能,求出點(diǎn)F的坐標(biāo);若不能,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,弦
的直徑,弦![]() 于
于![]() ,
,![]() 為
為![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() 交
交![]() 于
于![]() ,在
,在![]() 的延長(zhǎng)線上取一點(diǎn)
的延長(zhǎng)線上取一點(diǎn)![]() ,使
,使![]() ,
,![]() 的延長(zhǎng)線交
的延長(zhǎng)線交![]() 的延長(zhǎng)線于
的延長(zhǎng)線于![]() .
.
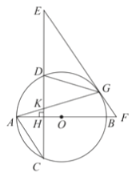
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)連接![]() ,若
,若![]() 時(shí).
時(shí).
①求證:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com