
【題目】如圖1,在平面直角坐標系中,拋物線y=![]() x2+
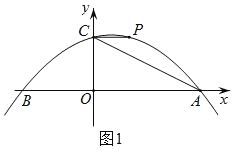
x2+![]() x+3與x軸交于A、B兩點(點A在點B的右側),與y軸交于點C,過點C作x軸的平行線交拋物線于點P.連接AC.
x+3與x軸交于A、B兩點(點A在點B的右側),與y軸交于點C,過點C作x軸的平行線交拋物線于點P.連接AC.
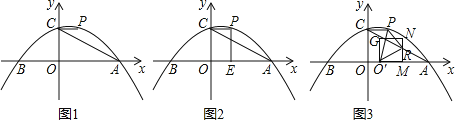
(1)求點P的坐標及直線AC的解析式;
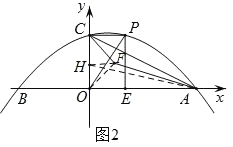
(2)如圖2,過點P作x軸的垂線,垂足為E,將線段OE繞點O逆時針旋轉得到OF,旋轉角為α(0°<α<90°),連接FA、FC.求AF+![]() CF的最小值;
CF的最小值;
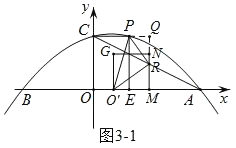
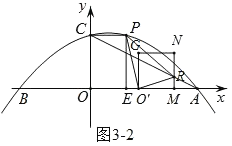
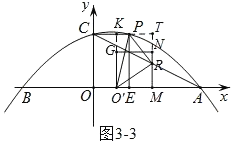
(3)如圖3,點M為線段OA上一點,以OM為邊在第一象限內作正方形OMNG,當正方形OMNG的頂點N恰好落在線段AC上時,將正方形OMNG沿x軸向右平移,記平移中的正方形OMNG為正方形O′MNG,當點M與點A重合時停止平移.設平移的距離為t,正方形O′MNG的邊MN與AC交于點R,連接O′P、O′R、PR,是否存在t的值,使△O′PR為直角三角形?若存在,求出t的值;若不存在,請說明理由.
【答案】(1)P(2,3),yAC=﹣![]() x+3;(2)
x+3;(2)![]() ;(3)存在,t的值為
;(3)存在,t的值為![]() ﹣3或
﹣3或![]() ,理由見解析
,理由見解析
【解析】
(1)由拋物線y=![]() x2+
x2+![]() x+3可求出點C,P,A的坐標,再用待定系數法,可求出直線AC的解析式;
x+3可求出點C,P,A的坐標,再用待定系數法,可求出直線AC的解析式;
(2)在OC上取點H(0,![]() ),連接HF,AH,求出AH的長度,證△HOF∽△FOC,推出HF=
),連接HF,AH,求出AH的長度,證△HOF∽△FOC,推出HF=![]() CF,由AF+
CF,由AF+![]() CF=AF+HF≥AH,即可求解;
CF=AF+HF≥AH,即可求解;
(3)先求出正方形的邊長,通過△ARM∽△ACO將相關線段用含t的代數式表示出來,再分三種情況進行討論:當∠O'RP=90°時,當∠PO'R=90°時,當∠O'PR=90°時,分別構造相似三角形,即可求出t的值,其中第三種情況不存在,舍去.
(1)在拋物線y=![]() x2+
x2+![]() x+3中,
x+3中,
當x=0時,y=3,
∴C(0,3),
當y=3時,x1=0,x2=2,
∴P(2,3),
當y=0時,則![]() x2+
x2+![]() x+3=0,
x+3=0,
解得:x1=﹣4,x2=6,
B(﹣4,0),A(6,0),
設直線AC的解析式為y=kx+3,
將A(6,0)代入,
得,k=﹣![]() ,
,
∴y=﹣![]() x+3,
x+3,
∴點P坐標為P(2,3),直線AC的解析式為y=﹣![]() x+3;
x+3;
(2)在OC上取點H(0,![]() ),連接HF,AH,
),連接HF,AH,
則OH=![]() ,AH=
,AH=![]() ,
,
∵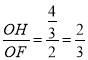 ,
,![]() ,且∠HOF=∠FOC,
,且∠HOF=∠FOC,
∴△HOF∽△FOC,
∴![]() ,
,
∴HF=![]() CF,
CF,
∴AF+![]() CF=AF+HF≥AH=
CF=AF+HF≥AH=![]() ,
,
∴AF+![]() CF的最小值為
CF的最小值為![]() ;
;
(3)∵正方形OMNG的頂點N恰好落在線段AC上,
∴GN=MN,
∴設N(a,a),
將點N代入直線AC解析式,
得,a=﹣![]() a+3,
a+3,
∴a=2,
∴正方形OMNG的邊長是2,
∵平移的距離為t,
∴平移后OM的長為t+2,
∴AM=6﹣(t+2)=4﹣t,
∵RM∥OC,
∴△ARM∽△ACO,
∴![]() ,
,
即![]() ,
,
∴RM=2﹣![]() t,
t,
如圖3﹣1,當∠O'RP=90°時,延長RN交CP的延長線于Q,
∵∠PRQ+∠O'RM=90°,∠RO'M+∠O'RM=90°,
∴∠PRQ=∠RO'M,
又∵∠Q=∠O'MR=90°,
∴△PQR∽△RMO',
∴![]() ,
,
∵PQ=2+t-2=t,QR=3﹣RM=1+![]() t,
t,
∴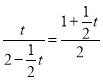 ,
,
解得,t1=﹣3﹣![]() (舍去),t2=
(舍去),t2=![]() ﹣3;
﹣3;
如圖3﹣2,當∠PO'R=90°時,
∵∠PO'E+∠RO'M=90°,∠PO'E+∠EPO'=90°,
∴∠RO'M=∠EPO',
又∵∠PEO'=∠O'MR=90°,
∴△PEO'∽△O'MR,
∴![]() ,
,
即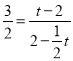 ,
,
解得,t=![]() ;
;
如圖3﹣3,當∠O'PR=90°時,延長O’G交CP于K,延長MN交CP的延長線于點T,
∵∠KPO'+∠TPR=90°,∠KO'P+∠KPO'=90°,
∴∠KO'P=∠TPR,
又∵∠O'KP=∠T=90°,
∴△KO'P∽△TPR,
∴![]() ,
,
即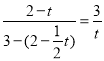 ,
,
整理,得t2-![]() t+3=0,
t+3=0,
∵△=b2﹣4ac=﹣![]() <0,
<0,
∴此方程無解,故不存在∠O'PR=90°的情況;
綜上所述,△O′PR為直角三角形時,t的值為![]() ﹣3或
﹣3或![]() .
.


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:
【題目】已知一個矩形紙片![]() ,將該紙片放置在平面直角坐標系中,點
,將該紙片放置在平面直角坐標系中,點![]() ,點
,點![]() ,點P為
,點P為![]() 邊上的動點.
邊上的動點.
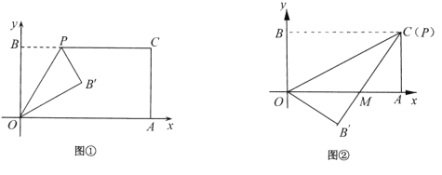
(1)如圖①,經過點O、P折疊該紙片,得點![]() 和折痕
和折痕![]() .當點P的坐標為
.當點P的坐標為![]() 時,求
時,求![]() 的度數;
的度數;
(2)如圖②,當點P與點C重合時,經過點O、P折疊紙片,使點B落在點![]() 的位置,
的位置,![]() 與
與![]() 交于點M,求點M的坐標;
交于點M,求點M的坐標;
(3)過點P作直線![]() ,交
,交![]() 于點Q,再取
于點Q,再取![]() 中點T,
中點T,![]() 中點N,分別以
中點N,分別以![]() ,
,![]() ,
,![]() ,
,![]() 為折痕,依次折疊該紙片,折疊后點O的對應點與點B的對應點恰好重合,且落在線段
為折痕,依次折疊該紙片,折疊后點O的對應點與點B的對應點恰好重合,且落在線段![]() 上,A、C的對應點也恰好重合,也落在線段
上,A、C的對應點也恰好重合,也落在線段![]() 上,求此時點P的坐標(直接寫出結果即可).
上,求此時點P的坐標(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在綠化某縣城與高速公路的連接路段中,需購買羅漢松、雪松兩種樹苗共400株,羅漢松樹苗每株60元,雪松樹苗每株70元.相關資料表明:羅漢松、雪松樹苗的成活率分別為70%,90%.
(1)若購買這兩種樹苗共用去26500元,則羅漢松、雪松樹苗各購買多少株?
(2)綠化工程來年一般都要將死樹補上新苗,現要使該兩種樹苗來年共補苗不多于80株,則羅漢松樹苗至多購買多少株?
(3)在(2)的條件下,應如何選購樹苗,才能使購買樹苗的費用最低?請求出最低費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,已知AB=2 ![]() ,AD=2,點P是對角線BD上一動點(不與B,D重合),連接AP,過點P作PE⊥AP,交DC于點E,
,AD=2,點P是對角線BD上一動點(不與B,D重合),連接AP,過點P作PE⊥AP,交DC于點E,
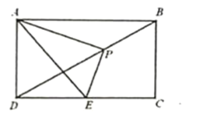
(1)求證:∠PAD=∠PEC;
(2)當點P是BD的中點時,求DE的值;
(3)在點P運動過程中,當DE= ![]() 時,求BP的值.
時,求BP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校“心靈信箱”的設立,為師、生之間的溝通開設了一個書面交流的渠道.為了解九年級學生對“心靈信箱”開通兩年來的使用情況,某課題組對該校九年級全體學生進行了一次問卷調查,并根據調查結果繪制了如下尚不完整的統計圖.
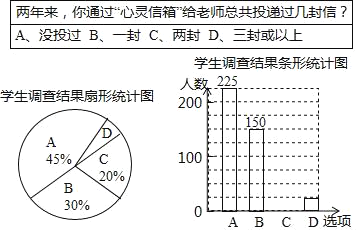
根據圖表,解答以下問題:
(1)該校九年級學生共有 人;
(2)學生調查結果扇形統計圖中,扇形D的圓心角度數是 ;
(3)請你補充條形統計圖;
(4)根據調查結果可以推斷:兩年來,該校九年級學生通過“心靈信箱”投遞出的信件總數至少有 封.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列各式規律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根據上面等式的規律:
(1)寫出第6個和第n個等式;
(2)證明你寫的第n個等式的正確性.
查看答案和解析>>
科目:初中數學 來源: 題型:
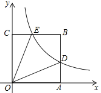
【題目】平面直角坐標系中,正方形OABC如圖放置,反比例函數![]() 的圖像交AB于點D,交BC于點E,已知A(
的圖像交AB于點D,交BC于點E,已知A(![]() ,0),∠DOE=30°,則k的值為( )
,0),∠DOE=30°,則k的值為( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年第七屆世界軍人運動會(7thCISMMilitaryWorldGames)于2019年10月18日至27日在中國武漢舉行,這是中國第一次承辦綜合性國際軍事賽事,也是繼北京奧運會后,中國舉辦的規模最大的國際體育盛會.某射擊運動員在一次訓練中射擊了10次,成績如圖所示.下列結論中不正確的有( )個
①眾數是8;②中位數是8;③平均數是8;④方差是1.6.
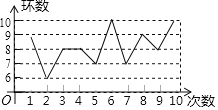
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是由邊長為![]() 的小正方形構成的網格,每個小正方形的頂點叫做格點.四邊形
的小正方形構成的網格,每個小正方形的頂點叫做格點.四邊形![]() 的頂點在格點上,點
的頂點在格點上,點![]() 是邊
是邊![]() 邊上的一點.請選擇適當的格點,用無刻度的直尺在網格中完成下列畫圖,保留連線的痕跡,不要求說明理由.
邊上的一點.請選擇適當的格點,用無刻度的直尺在網格中完成下列畫圖,保留連線的痕跡,不要求說明理由.
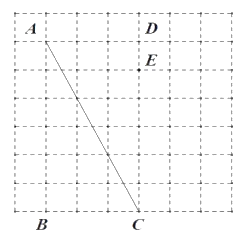
(1)①過![]() 作
作![]() 交
交![]() 邊于
邊于![]() ;
;
②過![]() 作
作![]() 于
于![]() 點;
點;
③在![]() 上作線段
上作線段![]()
(2)在(1)的條件下,連![]() ,若
,若![]() 為
為![]() 邊上的動點,在網格中求作一條線段
邊上的動點,在網格中求作一條線段![]() 等于
等于![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com