
【題目】為了滿足學生的物質需求,我市某中學到紅旗超市準備購進甲、乙兩種綠色袋裝食品.其中甲、乙兩種綠色袋裝食品的進價和售價如下表:
甲 | 乙 | |
進價(元/袋) |
|
|
售價(元/袋) | 20 | 13 |
已知:用2000元購進甲種袋裝食品的數量與用1600元購進乙種袋裝食品的數量相同.
(1)求![]() 的值;
的值;
(2)要使購進的甲、乙兩種綠色袋裝食品共800袋的總利潤(利潤=售價-進價)不少于5200元,且不超5280元,問該紅旗超市有幾種進貨方案?
(3)在(2)的條件下,該紅旗超市準備對甲種袋裝食品進行優惠促銷活動,決定對甲種袋裝食品每袋優惠![]() 元出售,乙種袋裝食品價格不變.那么該紅旗超市要獲得最大利潤應如何進貨?
元出售,乙種袋裝食品價格不變.那么該紅旗超市要獲得最大利潤應如何進貨?
【答案】(1)![]() ;(2)共有17種方案;(3)當
;(2)共有17種方案;(3)當![]() 時,
時,![]() 有最大值,即此時應購進甲種綠色袋裝食品240袋,表示出乙種綠色袋裝食品560袋.
有最大值,即此時應購進甲種綠色袋裝食品240袋,表示出乙種綠色袋裝食品560袋.
【解析】
(1)根據“用2000元購進甲種袋裝食品的數量與用1600元購進乙種袋裝食品的數量相同”列出方程并解答;
(2)設購進甲種綠色袋裝食品x袋,表示出乙種綠色袋裝食品(800-x)袋,然后根據總利潤列出一元一次不等式組解答;
(3)設總利潤為W,根據總利潤等于兩種綠色袋裝食品的利潤之和列式整理,然后根據一次函數的增減性分情況討論求解即可.
解:(1)依題意得:![]()
解得:![]() ,
,
經檢驗![]() 是原分式方程的解;
是原分式方程的解;
(2)設購進甲種綠色袋裝食品![]() 袋,表示出乙種綠色袋裝食品
袋,表示出乙種綠色袋裝食品![]() 袋,根據題意得,
袋,根據題意得,
![]()
解得:![]() ,
,
∵![]() 是正整數,
是正整數,![]() ,
,
∴共有17種方案;
(3)設總利潤為![]() ,則
,則![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 隨
隨![]() 的增大而增大,
的增大而增大,
所以,當![]() 時,
時,![]() 有最大值,
有最大值,
即此時應購進甲種綠色袋裝食品256袋,乙種綠色袋裝食品544袋;
②當![]() 時,
時,![]() ,(2)中所有方案獲利都一樣;
,(2)中所有方案獲利都一樣;
③當![]() 時,
時,![]() ,
,![]() 隨
隨![]() 的增大而減小,
的增大而減小,
所以,當![]() 時,
時,![]() 有最大值,
有最大值,
即此時應購進甲種綠色袋裝食品240袋,表示出乙種綠色袋裝食品560袋.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知點 C為線段 AB上一點,分別以 AC、BC為邊在線段 AB同側作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直線 AE與 BD交于點 F
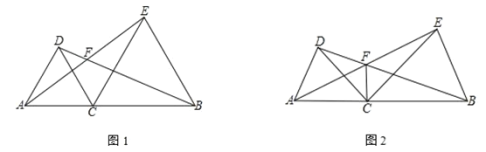
(1)如圖 1,若∠ACD=60°,則∠AFD=
(2)如圖 2,若∠ACD=α,連接 CF,則∠AFC= (用含α的式子表示)
(3) 將圖 1 中的△ACD繞點 C順時針旋轉如圖 3,連接 AE、AB、BD,∠ABD=80°,求∠EAB的度數
查看答案和解析>>
科目:初中數學 來源: 題型:
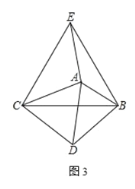
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() .點
.點![]() 從
從![]() 向
向![]() 以每秒
以每秒![]() 個單位的速度運動,以
個單位的速度運動,以![]() 為一邊在
為一邊在![]() 的右下方作正方形
的右下方作正方形![]() .同時垂直于
.同時垂直于![]() 的直線
的直線![]() 從
從![]() 向
向![]() 以每秒
以每秒![]() 個單位的速度運動,設運動時間為
個單位的速度運動,設運動時間為![]() 秒,當
秒,當![]() ________.秒時,直線
________.秒時,直線![]() 和正方形
和正方形![]() 開始有公共點
開始有公共點
查看答案和解析>>
科目:初中數學 來源: 題型:
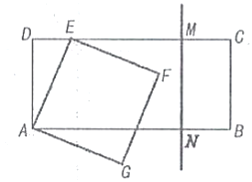
【題目】已知A、B、C為數軸上三點,若點C到點A的距離是點C到點B的距離的2倍,則稱點C是(A,B)的奇異點,例如圖1中,點A表示的數為﹣1,點B表示的數為2,表示1的點C到點A的距離為2,到點B的距離為1,則點C是(A,B)的奇異點,但不是(B,A)的奇異點.
(1)在圖1中,直接說出點D是(A,B)還是(B,C)的奇異點;
(2)如圖2,若數軸上M、N兩點表示的數分別為﹣2和4,
①若(M,N)的奇異點K在M、N兩點之間,則K點表示的數是 ;
②若(M,N)的奇異點K在點N的右側,請求出K點表示的數.
(3)如圖3,A、B在數軸上表示的數分別為﹣20和40,現有一點P從點B出發,向左運動.若點P到達點A停止,則當點P表示的數為多少時,P、A、B中恰有一個點為其余兩點的奇異點?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有大小兩種盛酒的桶,已知10個大桶加上2個小桶可以盛酒6斛(斛,音hu,是古代的一種容量單位),3個大桶加上15個小桶也可以盛酒6斛.
(1)求1個大桶可盛酒多少斛?
(2)分析2個大桶加上3個小桶可以盛酒2斛嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數![]() 的圖象分別交
的圖象分別交![]() 軸、
軸、![]() 軸于
軸于![]() 、
、![]() 兩點,點
兩點,點![]() 從點
從點![]() 出發沿
出發沿![]() 方向以每秒
方向以每秒![]() 個單位長度的速度向點
個單位長度的速度向點![]() 勻速運動,同時點
勻速運動,同時點![]() 從點
從點![]() 出發沿
出發沿![]() 方向以每秒2個單位長度向點
方向以每秒2個單位長度向點![]() 勻速運動,當其中一點到達終點時,另一點也停止運動,設運動時間為
勻速運動,當其中一點到達終點時,另一點也停止運動,設運動時間為![]() 秒,過點
秒,過點![]() 作
作![]() 軸,連接
軸,連接![]() 、
、![]() .
.
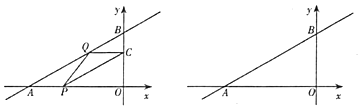
(1)點![]() 的坐標為________,點
的坐標為________,點![]() 的坐標為________,
的坐標為________,![]() ________;
________;
(2)四邊形![]() 能夠成為菱形嗎?如果能,求出相應的值;如果不能,說明理由.
能夠成為菱形嗎?如果能,求出相應的值;如果不能,說明理由.
(3)若點![]() ,點
,點![]() 在
在![]() 軸上,直線
軸上,直線![]() 上是否存在點
上是否存在點![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形?若存在,請直接寫出
為頂點的四邊形是平行四邊形?若存在,請直接寫出![]() 點的坐標;若不存在,說明理由.
點的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,過
,過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() .
.
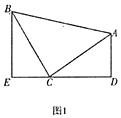
(1)求證:![]() .
.
(2)已知直線![]() 與
與![]() 軸交于
軸交于![]() 點,將直線
點,將直線![]() 繞著
繞著![]() 點順時針旋轉45°至
點順時針旋轉45°至![]() ,如圖2,求
,如圖2,求![]() 的函數解析式.
的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】省城太原某大型超市計劃在12月23日推出“十周年”店慶促銷活動,該超市為本次促銷活動設計了兩種促銷方案.方案一:全場商品全部打8.5折;方案二:商品總價不超過200元時,不打折,超過200元時,超過的部分打7折.小穎和爸爸媽媽準備在該超市促銷活動期間去該超市購物,所購商品總價一定會超過200元.
(1)小穎和爸爸媽媽購買的商品總價為![]() 元,按方案一應該支付 元;按方案二應該支付 元;(用含
元,按方案一應該支付 元;按方案二應該支付 元;(用含![]() 的代數式表示)
的代數式表示)
(2)當小穎和爸爸媽媽購買的商品總價為多少元時,按方案一或方案二支付的金額都一樣?
(3)若小穎和爸爸媽媽購買的商品總價為500元,請你幫助小穎計算一下,按哪種方案支付更劃算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某高中進行“選科走班”教學改革,語文、數學、英語三門為必修學科,另外還需從物理、化學、生物、政治、歷史、地理(分別記為A、B、C、D、E、F)六門選修學科中任選三門,現對該校某班選科情況進行調查,對調查結果進行了分析統計,并制作了兩幅不完整的統計圖.
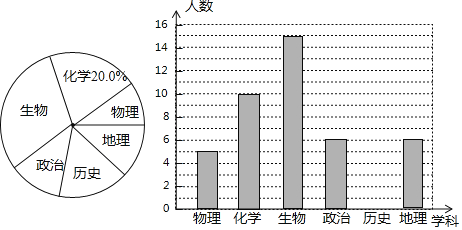
請根據以上信息,完成下列問題:
(1)該班共有學生人;
(2)請將條形統計圖補充完整;
(3)該班某同學物理成績特別優異,已經從選修學科中選定物理,還需從余下選修學科中任意選擇兩門,請用列表或畫樹狀圖的方法,求出該同學恰好選中化學、歷史兩科的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com