
【題目】如圖,在△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足為D點,AE平分∠BAC,交BD于點F交BC于點E,點G為AB的中點,連接DG,交AE于點H,下列結論錯誤的是( )
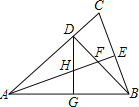
A.AH=2DFB.HE=BEC.AF=2CED.DH=DF
【答案】A
【解析】
通過證明△ADF≌△BDC,可得AF=BC=2CE,由等腰直角三角形的性質可得AG=BG,DG⊥AB,由余角的性質可得∠DFA=∠AHG=∠DHF,可得DH=DF,由線段垂直平分線的性質可得AH=BH,可求∠EHB=∠EBH=45°,可得HE=BE,即可求解.
解:∵∠BAC=45°,BD⊥AC,
∴∠CAB=∠ABD=45°,
∴AD=BD,
∵AB=AC,AE平分∠BAC,
∴CE=BE=![]() BC,∠CAE=∠BAE=22.5°,AE⊥BC,
BC,∠CAE=∠BAE=22.5°,AE⊥BC,
∴∠C+∠CAE=90°,且∠C+∠DBC=90°,
∴∠CAE=∠DBC,且AD=BD,∠ADF=∠BDC=90°,
∴△ADF≌△BDC(AAS)
∴AF=BC=2CE,故選項C不符合題意,
∵點G為AB的中點,AD=BD,∠ADB=90°,∠CAE=∠BAE=22.5°,
∴AG=BG,DG⊥AB,∠AFD=67.5°
∴∠AHG=67.5°,
∴∠DFA=∠AHG=∠DHF,
∴DH=DF,故選項D不符合題意,
連接BH,
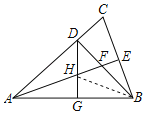
∵AG=BG,DG⊥AB,
∴AH=BH,
∴∠HAB=∠HBA=22.5°,
∴∠EHB=45°,且AE⊥BC,
∴∠EHB=∠EBH=45°,
∴HE=BE,
故選項B不符合題意,
故選:A.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知點A(﹣2,0),B(3,0).
(1)在y軸上找一點C,使之滿足△ABC的面積為12,求點C的坐標.
(2)在y軸上找一點D,使BD=AB,求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某鎮的一種特產由于運輸原因,長期只能在當地銷售.當地政府對該特產的銷售投資收益為:每投入x萬元,可獲得利潤![]() 當地政府擬在“十二五”規劃中加快開發該特產的銷售,其規劃方案為:在規劃前后對該項目每年最多可投入100萬元的銷售投資,在實施規劃5年的前兩年中,每年都從100萬元中撥出50萬元用于修建一條公路,兩年修成,通車前該特產只能在當地銷售;公路通車后的3年中,該特產既在本地銷售,也在外地銷售.在外地銷售的投資收益為:每投入x萬元,可獲利潤
當地政府擬在“十二五”規劃中加快開發該特產的銷售,其規劃方案為:在規劃前后對該項目每年最多可投入100萬元的銷售投資,在實施規劃5年的前兩年中,每年都從100萬元中撥出50萬元用于修建一條公路,兩年修成,通車前該特產只能在當地銷售;公路通車后的3年中,該特產既在本地銷售,也在外地銷售.在外地銷售的投資收益為:每投入x萬元,可獲利潤![]()
(1)若不進行開發,求5年所獲利潤的最大值是多少?
(2)若按規劃實施,求5年所獲利潤(扣除修路后)的最大值是多少?
(3)根據(1)、(2),該方案是否具有實施價值?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)如圖,在五邊形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求證:△ABC≌△AED;
(2)當∠B=140°時,求∠BAE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
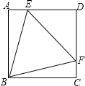
【題目】如圖,正方形![]() 中,點
中,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,且
上,且![]() 為等邊三角形,下列結論:
為等邊三角形,下列結論:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正確的結論個數有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把![]() 和
和![]() 按如圖
按如圖![]() 擺放(點
擺放(點![]() 與
與![]() 重合),點
重合),點![]() 、
、![]() 、
、![]() 在同一條直線上.已知:
在同一條直線上.已知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如圖
.如圖![]() ,
,![]() 從圖
從圖![]() 的位置出發,以
的位置出發,以![]() 的速度沿
的速度沿![]() 向
向![]() 勻速移動,在
勻速移動,在![]() 移動的同時,點
移動的同時,點![]() 從
從![]() 的頂點
的頂點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 勻速移動;當點
勻速移動;當點![]() 移動到點
移動到點![]() 時,點
時,點![]() 停止移動,
停止移動,![]() 也隨之停止移動.
也隨之停止移動.![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() ,設移動時間為
,設移動時間為![]() .
.
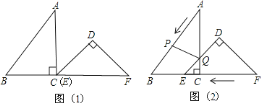
![]() 用含
用含![]() 的代數式表示線段
的代數式表示線段![]() 和
和![]() 的長,并寫出
的長,并寫出![]() 的取值范圍;
的取值范圍;
![]() 當
當![]() 為何值時,
為何值時,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD,AC與BD交于點E,∠ADB=∠ACB.
(1)求證:![]() ;
;
(2)若AB⊥AC,AE:EC=1:2,F是BC中點,求證:四邊形ABFD是菱形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com