
【題目】如圖,矩形ABCD中,E為BC上一點,DF⊥AE于F.
(1)ΔABE與ΔADF相似嗎?請說明理由.
(2)若AB=6,AD=12,BE=8,求FD的長.

【答案】(1)、相似,證明過程見解析;(2)、FD=7.2
【解析】
試題分析:(1)、首先根據矩形和DF⊥AE可得∠B=∠AFD,根據AD∥BC可得∠DAF=∠AEB,從而得出三角形相似;(2)、首先根據Rt△ABE的勾股定理求出AE的長度,然后根據三角形相似得出DF的長度.
試題解析:(1)、∵ABCD為矩形 ∴∠BAD=∠B=90° ∵DF⊥AE ∴∠AFD=90°
∵AD∥BC ∴∠DAF=∠AEB 在△ABE和△AFD中 ∠B=∠AFD,∠DAF=∠AEB ∴△ABE∽△ADF
(2)、∵AB=6,BE=8,∠B=90° ∴AE=10 ∵△ABE∽△ADF ∴![]()
∴![]() ∴DF=7.2
∴DF=7.2


科目:初中數學 來源: 題型:
【題目】某校為了豐富校園文化,舉行初中生書法大賽,決賽設置了7個獲獎名額,共有13名選手進入決賽,選手決賽得分均不相同,小穎知道自己的比賽分數后,要判斷自己能否獲獎,需要知道這13名同學成績的( )
A.眾數B.中位數C.平均數D.方差
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系中,△ABC的頂點都在網格點上,其中,C點坐標為(1,2)
(1)寫出點A、B的坐標:A( , )、B( , )
(2)將△ABC先向左平移1個單位長度,再向上平移2個單位長度,得到△A′B′C′,畫出△A′B′C′
(3)寫出三個頂點坐標A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題: 小明和同學去公園春游.在公園門口看到公園的公告如圖.
(1)如果小明他們共19人,那么他們買19張5元的門票省錢,還是買1張20人的團體票省錢?請說明理由.
(2)如果小明他們買1張20人的團體票,比每人買1張5元的門票總共少花了10元,你能求出小明他們共有多少人嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
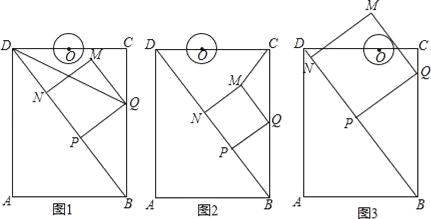
【題目】如圖,在矩形ABCD中,AB=6cm,AD=8cm,點P從點B出發,沿對角線BD向點D勻速運動,速度為4cm/s,過點P作PQ⊥BD交BC于點Q,以PQ為一邊作正方形PQMN,使得點N落在射線PD上,點O從點D出發,沿DC向點C勻速運動,速度為3m/s,以O為圓心,0.8cm為半徑作⊙O,點P與點O同時出發,設它們的運動時間為t(單位:s)(0<t<![]() ).
).
(1)如圖1,連接DQ平分∠BDC時,t的值為 ;
(2)如圖2,連接CM,若△CMQ是以CQ為底的等腰三角形,求t的值;
(3)請你繼續進行探究,并解答下列問題:
①證明:在運動過程中,點O始終在QM所在直線的左側;
②如圖3,在運動過程中,當QM與⊙O相切時,求t的值;并判斷此時PM與⊙O是否也相切?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com