
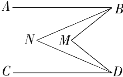
【題目】如圖,AB∥CD,BN,DN分別平分∠ABM,∠MDC,試問∠M與∠N之間的數量關系如何?請說明理由.
【答案】∠N=![]() ∠M
∠M
【解析】
過點M作直線ME∥AB,過點N作直線NF∥AB,由平行線的性質可得∠BMD=ABM+∠CDM,∠BND=∠ABN+∠CDN,再根據角平分線的性質,即可得到∠BMD和∠BND的關系.
解:∠BMD=2∠BND.理由如下:
過點M作直線ME∥AB,過點N作直線NF∥AB,
又∵AB∥CD,
∴ME∥CD,NF∥CD(平行于同一直線的兩直線互相平行),
∴∠ABM=∠BME,∠CDM=∠DME(兩直線平行,內錯角相等),
∴∠BMD=∠BME+∠DME=∠ABM+∠CDM.
同理可得:∠BND=∠ABN+∠CDN.
∵BN,DN分別平分∠ABM,∠MDC,
∴∠ABM=2∠ABN,∠CDM=2∠CDN(角平分線定義)
∴∠BMD=2∠BND.即∠N=![]() ∠M
∠M


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖1,直線l:y=![]() x+m與x軸、y軸分別交于點A和點B(0,﹣1),拋物線y=
x+m與x軸、y軸分別交于點A和點B(0,﹣1),拋物線y=![]() x2+bx+c經過點B,與直線l的另一個交點為C(4,n).
x2+bx+c經過點B,與直線l的另一個交點為C(4,n).
(1)求n的值和拋物線的解析式;
(2)點D在拋物線上,DE∥y軸交直線l于點E,點F在直線l上,且四邊形DFEG為矩形(如圖2),設點D的橫坐標為t(0<t<4),矩形DFEG的周長為p,求p與t的函數關系式以及p的最大值;
(3)將△AOB繞平面內某點M旋轉90°或180°,得到△A1O1B1,點A、O、B的對應點分別是點A1、O1、B1.若△A1O1B1的兩個頂點恰好落在拋物線上,那么我們就稱這樣的點為“落點”,請直接寫出“落點”的個數和旋轉180°時點A1的橫坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只不透明的袋子中裝有3個球,球上分別標有數字0,1,2,這些球除了數字外其余都相同,甲、以兩人玩摸球游戲,規則如下:先由甲隨機摸出一個球(不放回),再由乙隨機摸出一個球,兩人摸出的球所標的數字之和為偶數時則甲勝,和為奇數時則乙勝.
(1)用畫樹狀圖或列表的方法列出所有可能的結果;
(2)這樣的游戲規則是否公平?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車廠計劃一周生產自行車1400輛,由于種種原因,每天生產量不同.下表是某周的生產變化情況,上周日生產200輛(正數表示比前一天多生產的輛數,負數表示比前一天少生產的輛數):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
輛數變化(單位:輛) |
|
|
|
|
|
|
|
(1)根據記錄的數據可知該廠這周星期四生產了多少輛自行車?
(2)這周產量最多的一天比產量最少的一天多生產了多少輛自行車?
(3)根據記錄的數據可知該廠本周實際生產了多少輛自行車?
(4)該廠實行每周計件工資制,每生產一輛車可得50元,若超額完成任務,則超過部分每輛另外獎勵20元,少生產一輛扣25元,那么該廠工人這一周的工資總額是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
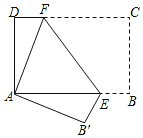
【題目】如圖,將長方形紙片ABCD折疊,使點C與點A重合,折痕EF分別與AB、DC交于點E和點F.
(1)試寫出圖中若干相等的線段和銳角(分別寫兩對);
(2)證明:△ADF≌△AB′E.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程![]() ,下列說法正確的是( )
,下列說法正確的是( )
A. 當k=0時,方程沒有實數根 B. 當k=1時,方程有一個實數根
C. 當k=-1時,方程有兩個相等的實數根 D. 當k≠0時,方程總有兩個不相等的實數根
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,∠BAC=56°,點D為AB中點,且OD⊥AB,∠BAC的平分線與AB的垂直平分線交于點O,將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合則∠OEC為_____.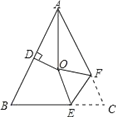
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】①![]() 的解
的解![]() .
.
②![]() 的解
的解![]() .
.
③![]() 的解
的解![]() .
.
④![]() 的解
的解![]() .…
.…
(1)根據你發現的規律直接寫出第⑤,⑥個方程及它們的解.
⑤
⑥
(2)請根據你發現的規律直接寫出第![]() 個方程及它的解,并通過計算判斷這個結論是否正確.
個方程及它的解,并通過計算判斷這個結論是否正確.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com