
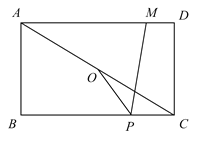
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,連接
,連接![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 上一點,且
上一點,且![]() ,
,![]() 是
是![]() 上一動點,則
上一動點,則![]() 的最大值為__________.
的最大值為__________.
【答案】![]()
【解析】
連接MO并延長交BC于P,則此時,PMPO的值最大,且PMPO的最大值=OM,根據全等三角形的性質得到AM=CP=4,OM=OP,求得PB=1,過M作MN⊥BC于N,得到四邊形MNCD是矩形,得到MN=CD,CN=DM,根據勾股定理即可得到結論.
∵在矩形ABCD中,AD=5,MD=1,
∴AM=ADDM=51=4,
連接MO并延長交BC于P,
則此時,PMPO的值最大,且PMPO的最大值=OM,
∵AM∥CP,
∴∠MAO=∠PCO,
∵∠AOM=∠COP,AO=CO,
∴△AOM≌△COP(ASA),
∴AM=CP=4,OM=OP,
∴PB=54=1,
過M作MN⊥BC于N,
∴四邊形MNCD是矩形,
∴MN=CD=AB=4,CN=DM=1,
∴PN=511=3,
∴MP=![]() =
=![]() =5,
=5,
∴OM=![]() MP=
MP=![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2﹣2和x軸交于A,B(點A在點B右邊)兩點,和y軸交于點C,P為拋物線上的動點.
(1)求出A,C的坐標;
(2)求動點P到原點O的距離的最小值,并求此時點P的坐標;
(3)當點P在x軸下方的拋物線上運動時,過P的直線交x軸于E,若△POE和△POC全等,求此時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P是半圓O中![]() 所對弦AB上一動點,過點P作PM⊥AB交
所對弦AB上一動點,過點P作PM⊥AB交![]() 于點M,作射線PN交
于點M,作射線PN交![]() 于點N,使得∠NPB=45°,連接MN.已知AB=6cm,設A,P兩點間的距離為xcm,M,N兩點間的距離為ycm.(當點P與點A重合時,點M也與點A重合,當點P與點B重合時,y的值為0)
于點N,使得∠NPB=45°,連接MN.已知AB=6cm,設A,P兩點間的距離為xcm,M,N兩點間的距離為ycm.(當點P與點A重合時,點M也與點A重合,當點P與點B重合時,y的值為0)
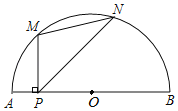
小超根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小超的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,得到了y與x的幾組對應值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4.2 | 2.9 | 2.6 | 2.0 | 1.6 | 0 |
(說明:補全表格時相關數值保留一位小數)
(2)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題:當MN=2AP時,AP的長度約為 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
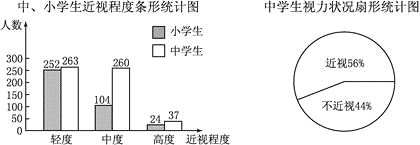
【題目】某市青少年健康研究中心隨機抽取了本市1000名小學生和若干名中學生,對他們的視力狀況進行了調查,并把調查結果繪制成如下統計圖.(近視程度分為輕度、中度、高度三種)
(1)求這1000名小學生患近視的百分比.
(2)求本次抽查的中學生人數.
(3)該市有中學生8萬人,小學生10萬人.分別估計該市的中學生與小學生患“中度近視”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于A(1,t+1),B(t-5,-1)兩點.
的圖象交于A(1,t+1),B(t-5,-1)兩點.
(1)求一次函數和反比例函數的解析式;
(2)若點(c,p)和(n,q)是反比例函數y=![]() 圖象上任意兩點,且滿足c=n+1時,求
圖象上任意兩點,且滿足c=n+1時,求![]() 的值.
的值.
(3)若點M(x1,y1)和N(x2,y2)在直線AB(不與A、B重合)上,過M、N兩點分別作y軸的平行線交雙曲線于E、F,已知x1<-3,0<x2<1,當x1x2=-3時,判斷四邊形NFEM的形狀.并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點![]() (
(![]() ,1)為函數
,1)為函數![]() (
(![]() ,
,![]() 為常數,且
為常數,且![]() )與
)與![]() 的圖象的交點.
的圖象的交點.
(1)求![]() ;
;
(2)若函數![]() 的圖象與
的圖象與![]() 軸只有一個交點,求
軸只有一個交點,求![]() ,
,![]() ;
;
(3)若![]() ,設當
,設當![]() 時,函數
時,函數![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
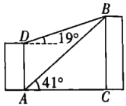
【題目】如圖,已知一居民樓![]() 前方
前方![]() 處有一建筑物
處有一建筑物![]() ,小敏在居民樓的頂部
,小敏在居民樓的頂部![]() 處和底部
處和底部![]() 處分別測得建筑物頂部
處分別測得建筑物頂部![]() 的仰角為
的仰角為![]() 和
和![]() ,求居民樓的高度
,求居民樓的高度![]() 和建筑物的高度
和建筑物的高度![]() (結果取整數).
(結果取整數).
(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
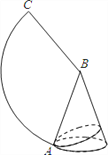
【題目】如圖,已知圓錐的底面半徑是2,母線長是6.
(1)求這個圓錐的高和其側面展開圖中∠ABC的度數;
(2)如果A是底面圓周上一點,從點A拉一根繩子繞圓錐側面一圈再回到A點,求這根繩子的最短長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】距離中考體考時間越來越近,年級想了解初三年級1000名學生周末在家體育鍛煉的情況,在初三年級隨機抽取了20名男生和20名女生,對他們周末在家的鍛煉時間進行了調查,并收集得到了以下數據(單位:min):
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
統計數據,并制作了如下統計表:
時間 x | x≤30 | 30<x≤60 | 60<x≤90 | 90<x≤120 | |
男生 | 2 | 8 | 8 | 2 | |
女生 | 1 | m | n | 3 |
分析數據:兩組數據的極差、平均數、中位數、眾數如下表所示
極差 | 平均數 | 中位數 | 眾數 | |
男生 | a | 65.75 | b | 90 |
女生 | c | 75.5 | 75 | d |
(1)請將上面的表格補充完整:m= ,n= ,a= ,b= ,c= ,d=
(2)已知該年級男女生人數差不多,根據調查的數據,估計初三年級周末在家鍛煉的時間在 90min 以上的同學約有多少人?
(3)李老師看了表格數據后認為初三年級的女生周末鍛煉做得比男生好,請你結合統計數據,寫出兩條支持李老師觀點的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com