
【題目】如圖,![]() 是
是![]() 的邊
的邊![]() 上一點,
上一點,![]() ,
,![]() 交
交![]() 于點
于點![]() ,若
,若![]() .
.
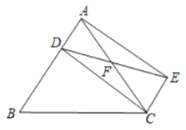
(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)若![]() ,
,![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
【答案】(1)證明見解析;(2)25![]() .
.
【解析】
(1)首先利用ASA得出△DAF≌△ECF,進而利用全等三角形的性質得出CE=AD,即可得出四邊形ACDE是平行四邊形;
(2)由AE⊥EC,四邊形ADCE是平行四邊形,可推出四邊形ADCE是矩形,由F為AC的中點,求出AC,根據勾股定理即可求得AE,由矩形面積公式即可求得結論.
解:(1)證明:∵CE∥AB,
∴∠BAC=∠ECA,
在△DAF和△ECF中,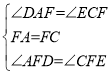 ,
,
∴△DAF≌△ECF(ASA),
∴CE=AD,
∴四邊形ADCE是平行四邊形;
(2)∵AE⊥EC,四邊形ADCE是平行四邊形,
∴四邊形ADCE是矩形,
在Rt△AEC中,F為AC的中點,
∴AC=2EF=10,
∴AE2=AC2-EC2=102-52=75,
∴AE=5![]() ,
,
∴四邊形ADCE的面積=AEEC=25![]() .
.


科目:初中數學 來源: 題型:
【題目】小濤根據學習函數的經驗,對函數![]() 的圖像與性質進行了探究,下面是小濤的探究過程,請補充完整:
的圖像與性質進行了探究,下面是小濤的探究過程,請補充完整:
(1)下表是![]() 與
與![]() 的幾組對應值
的幾組對應值
| ... | -2 | -1 | 0 | 1 | 2 |
| 3 | ... |
| ... | -8 | -3 | 0 | m | n | 1 | 3 | ... |
請直接寫出:![]() =, m=, n=;
=, m=, n=;
(2)如圖,小濤在平面直角坐標系中,描出了上表中已經給出的部分對應值為坐標的點,再描出剩下的點,并畫出該函數的圖象;
(3)請直接寫出函數![]() 的圖像性質:;(寫出一條即可)
的圖像性質:;(寫出一條即可)
(4)請結合畫出的函數圖象,解決問題:若方程![]() 有三個不同的解,直接寫出
有三個不同的解,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著科技的進步和網絡資源的豐富,在線學習已經成為更多人自主學習的選擇.某校計劃為學生提供以下四類在線學習方式:在線閱讀、在線聽課、在線答題和在線討論.為了解學生需求,該校隨機對本校部分學生進行了“你對哪類在線學習方式最感興趣”的調查,并根據調查結果繪制成如下兩幅不完整的統計圖.
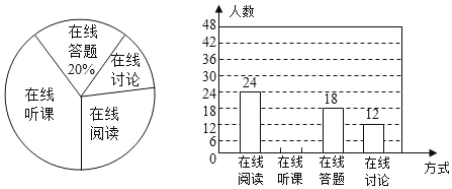
請你根據統計圖中提供的信息解答下列問題:
(1)求本次調查的學生總人數;
(2)通過計算補全條形統計圖;
(3)該校共有學生![]() 人,請你估計該校對在線閱讀最感興趣的學生有多少人.
人,請你估計該校對在線閱讀最感興趣的學生有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
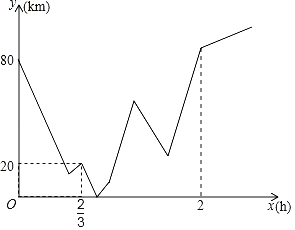
【題目】A、B兩地之間有一修理廠C,一日小海和王陸分別從A、B兩地同時出發相向而行,王陸開車,小海騎摩托.二人相遇時小海的摩托車突然出故障無法前行,王陸決定將小海和摩托車一起送回到修理廠C后再繼續按原路前行,王陸到達A地后立即返回B地,到B地后不再繼續前行,等待小海前來(裝載摩托車時間和掉頭時間忽略不計),整個行駛過程中王陸速度不變,而小海在修理廠花了十分鐘修好摩托車,為了趕時間,提速![]() 前往目的地B,小海到達B地后也結束行程,若圖象表示的是小海與王陸二人到修理廠C的距離和y(km)與小海出行時間之間x(h)的關系,則當王陸第二次與小海在行駛中相遇時,小海離目的地B還有_____km.
前往目的地B,小海到達B地后也結束行程,若圖象表示的是小海與王陸二人到修理廠C的距離和y(km)與小海出行時間之間x(h)的關系,則當王陸第二次與小海在行駛中相遇時,小海離目的地B還有_____km.
查看答案和解析>>
科目:初中數學 來源: 題型:
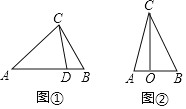
【題目】如圖1和圖2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如圖1,AH⊥BC于點H,則AH=___,AC=___,△ABC的面積![]() =___.
=___.
拓展:如圖2,點D在AC上(可與點A、C重合),分別過點A、C作直線BD的垂線,垂足為E、F,設BD=x,AE=m,CF=n,(當點D與A重合時,我們認為![]() =0).
=0).
(1)用含x、m或n的代數式表示![]() 及
及![]() ;
;
(2)求(m+n)與x的函數關系式,并求(m+n)的最大值和最小值;
(3)對給定的一個x值,有時只能確定唯一的點D,指出這樣的x的取值范圍.
發現:請你確定一條直線,使得A、B、C三點到這條直線的距離之和最小(不必寫出過程),并寫出這個最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019 年3月16日,由中國科協主辦的第六屆全國青年科普創新實驗暨作品大賽啟動,重點圍繞“智能、環保、教育”三大主題,某中學派出甲、乙兩組隊伍參加本次大賽,有四個命題供他們選擇:
①智能:智能控制及人工智能命題(用![]() 表示)
表示)
②環保:包括生物環境、風能兩個命題(分別用![]() 表示)
表示)
③教育:未來教育命題(用![]() 表示)
表示)
![]() 甲組隊伍在四個命題中隨機選取一個報名 ,恰好選擇“教育”主題的概率是多少?
甲組隊伍在四個命題中隨機選取一個報名 ,恰好選擇“教育”主題的概率是多少?
![]() 若甲,乙兩組隊伍各隨機從四個命題中選--個報名.請用樹狀圖法或列表法求出他們都選擇“環保”主題的概率.
若甲,乙兩組隊伍各隨機從四個命題中選--個報名.請用樹狀圖法或列表法求出他們都選擇“環保”主題的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①在![]() 中,若點
中,若點![]() 在邊
在邊![]() 上,且
上,且![]() 則點
則點![]() 定義為
定義為![]() 的邊
的邊![]() 上的“金點”.
上的“金點”.
![]() 已知點
已知點![]() 是
是![]() 的邊
的邊![]() 上的“金點”:
上的“金點”:
①若![]() 則
則![]() 的長為 _;
的長為 _;
②若![]() 則
則![]() 的長為 _;
的長為 _;
![]() 在圖①中,若點
在圖①中,若點![]() 是
是![]() 的邊
的邊![]() 的中點,
的中點,![]() 試判斷點
試判斷點![]() 是不是
是不是![]() 的“金
的“金
點”,并說明理由;
![]() 如圖②,已知點
如圖②,已知點![]() 為同一直線上三點,且
為同一直線上三點,且![]() 在
在![]() 所在直線上是否存在一點
所在直線上是否存在一點![]() 使點
使點![]() 中的某一點是其余三點圍成的三角形的“金點”.若存在,求出線段
中的某一點是其余三點圍成的三角形的“金點”.若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
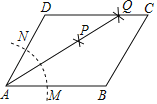
【題目】如圖,在平行四邊形ABCD中,按以下步驟作圖:①以A為圓心,任意長為半徑作弧,分別交AB,AD于點M,N;②分別以M,N為圓心,以大于![]() MN的長為半徑作弧,兩弧相交于點P;③作AP射線,交邊CD于點Q,若DQ=2QC,BC=3,則平行四邊形ABCD周長為________.
MN的長為半徑作弧,兩弧相交于點P;③作AP射線,交邊CD于點Q,若DQ=2QC,BC=3,則平行四邊形ABCD周長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
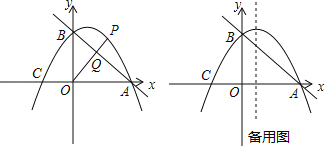
【題目】如圖,直線y=﹣![]() x+3與x軸交于點A,與y軸交于點B.拋物線y=﹣
x+3與x軸交于點A,與y軸交于點B.拋物線y=﹣![]() x2+bx+c經過A、B兩點,與x軸的另一個交點為C.
x2+bx+c經過A、B兩點,與x軸的另一個交點為C.
(1)求拋物線的解析式;
(2)點P是第一象限拋物線上的點,連接OP交直線AB于點Q.設點P的橫坐標為m,PQ與OQ的比值為y,求y與m的關系式,并求出PQ與OQ的比值的最大值;
(3)點D是拋物線對稱軸上的一動點,連接OD、CD,設△ODC外接圓的圓心為M,當sin∠ODC的值最大時,求點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com