
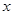 的一元二次方程
的一元二次方程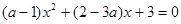 .
.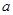 取不等于l的實數時,此方程總有兩個實數根.
取不等于l的實數時,此方程總有兩個實數根.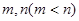 是此方程的兩根,并且
是此方程的兩根,并且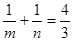 ,直線
,直線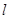 :
: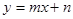 交
交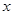 軸于點A,交
軸于點A,交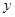 軸于點B,坐標原點O關于直線
軸于點B,坐標原點O關于直線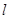 的對稱點O′在反比例函數
的對稱點O′在反比例函數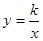 的圖象上,求反比例函數
的圖象上,求反比例函數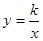 的解析式.
的解析式.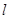 繞點A逆時針旋轉角
繞點A逆時針旋轉角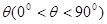 ,得到直線
,得到直線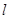 ′,
′,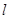 ′交
′交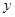 軸于點P,過點P作
軸于點P,過點P作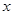 軸的平行線,與上述反比例函數
軸的平行線,與上述反比例函數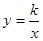 的圖象交于點Q,當四邊形APQO′的面積為
的圖象交于點Q,當四邊形APQO′的面積為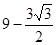 時,求角
時,求角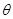 的值.
的值. 為關于
為關于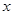 的一元二次方程
的一元二次方程 ,即
,即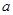 ≠1
≠1
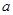 取不等于1的實數時,此方程總有兩個實數根.
取不等于1的實數時,此方程總有兩個實數根. ,
,
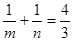

 、
、 是方程
是方程 的兩根
的兩根

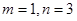
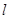 的解析式為
的解析式為
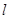 與
與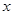 軸交點A(-3,0)與
軸交點A(-3,0)與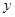 軸交點B(0,3)
軸交點B(0,3)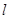 的對稱點O′的坐標為(-3,3)
的對稱點O′的坐標為(-3,3)
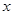 軸,與反比例函數圖象交于點Q
軸,與反比例函數圖象交于點Q ,P)
,P)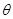 <45°,即P>3時
<45°,即P>3時 ,GO′=P-3,GA=P
,GO′=P-3,GA=P ×GA×GP-
×GA×GP- ×GQ×GO’
×GQ×GO’ ×P×3-
×P×3- (3
(3 )×(P-3)
)×(P-3)


 符合題意
符合題意 )
)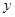 軸的對稱點A′(3,0),連結A′P,
軸的對稱點A′(3,0),連結A′P,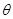 =∠PAO -∠BAO =60°-45°=15°
=∠PAO -∠BAO =60°-45°=15°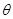 <90°,即P<-3時,
<90°,即P<-3時, ,這與P<-3矛盾,所以此時點P不存在
,這與P<-3矛盾,所以此時點P不存在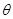 =15°
=15°
 ,再代入
,再代入 ,可得到a=2,則m=1,n=3,直線l:y=x+3,這樣就可得到坐標原點O關于直線l的對稱點,代入反比例函數y="k/x" ,即可確定反比例函數y="k/x" 的解析式;
,可得到a=2,則m=1,n=3,直線l:y=x+3,這樣就可得到坐標原點O關于直線l的對稱點,代入反比例函數y="k/x" ,即可確定反比例函數y="k/x" 的解析式; ,這樣可求出p;可得到OP,PA,可求出∠PAO=60°,這樣就可求出θ.
,這樣可求出p;可得到OP,PA,可求出∠PAO=60°,這樣就可求出θ.

 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com