
【題目】(本題滿分10分)如圖,將□ABCD沿過點A的直線![]() 折疊,使點D落到AB邊上的點
折疊,使點D落到AB邊上的點![]() 處,折痕
處,折痕![]() 交CD邊于點E,連接BE
交CD邊于點E,連接BE
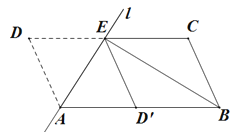
(1)求證:四邊形![]() 是平行四邊形
是平行四邊形
(2)若BE平分∠ABC,求證:![]()
【答案】見解析
【解析】試題(1)根據翻折變換的性質以及平行線的性質得出∠DAE=∠EAD′=∠DEA=∠D′EA,然后根據平行四邊形的判定方法得出四邊形DAD′E是平行四邊形,進而求出四邊形BCED′是平行四邊形;
(2)根據平行線的性質利用勾股定理得出答案.
試題解析:(1)∵將ABCD沿過點A的直線l折疊,使點D落到AB邊上的點D′處,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,∴∠DEA=∠EAD′,∴∠DAE=∠EAD′=∠DEA=∠D′EA,∴∠DAD′=∠DED′,
∴四邊形DAD′E是平行四邊形,∴DE=AD′,
∵四邊形ABCD是平行四邊形,∴AB![]() DC,∴CE
DC,∴CE![]() D′B,∴四邊形BCED′是平行四邊形;
D′B,∴四邊形BCED′是平行四邊形;
(2)∵BE平分∠ABC,∴∠CBE=∠EBA,
∵AD∥BC,∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,∴∠EAB+∠EBA=90°,∴∠AEB=90°,∴AB2=AE2+BE2.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,專業救助船“滬救1”輪、“滬救2”輪分別位于A、B兩處,同時測得事發地點C在A的南偏東60°且C在B的南偏東30°上.已知B在A的正東方向,且相距100里,請分別求出兩艘船到達事發地點C的距離.(注:里是海程單位,相當于一海里.結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠1+∠2﹦180°,∠3﹦∠B,則DE∥BC,下面是王華同學的推導過程﹐請你幫他在括號內填上推導依據或內容.

證明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校獎勵給王偉和李麗上海世博園門票共兩張,其中一張為指定日門票,另一張為普通日門票.班長由王偉和李麗分別轉動下圖的甲、乙兩個轉盤(轉盤甲被二等分、轉盤乙被三等分)確定指定日門票的歸屬,在兩個轉盤都停止轉動后,若指針所指的兩個數字之和為偶數,則王偉獲得指定日門票;若指針所指的兩個數字之和為奇數,則李麗獲得指定日門票;若指針指向分隔線,則重新轉動.你認為這個方法公平嗎?請畫樹狀圖或列表,并說明理由.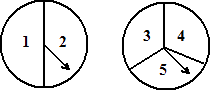
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從汽車燈的點O處發出的一束光線經燈的反光罩反射后沿CO方向平行射出,如入射光線OA的反射光線為AB,∠OAB=75°.在如圖中所示的截面內,若入射光線OD經反光罩反射后沿DE射出,且∠ODE=22°.則∠AOD的度數是_____.
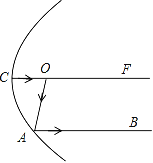
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是線段DE上一點,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求證:DE=BD+CE.
(2)如果是如圖2這個圖形,BD、CE、DE有什么數量關系?并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的正方形ABCD中剪去一個邊長為1的小正方形CEFG,動點P從點A出發,沿A→D→E→F→G→B的路線繞多邊形的邊勻速運動到點B時停止(不含點A和點B),則△ABP的面積S隨著時間t變化的函數圖像大致為( )
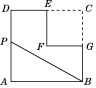
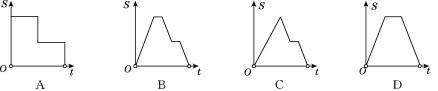
A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,點D是AB上一點,以BD為直徑的⊙O和AB相切于點P.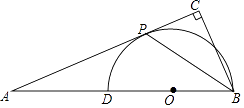
(1)求證:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com