
【題目】若二次函數y=ax2+bx﹣2的圖象與x軸交于點A(4,0),與y軸交于點B,且過點C (3,﹣2).

(1)求二次函數表達式;
(2)若點P為拋物線上第一象限內的點,且S△PBA=5,求點P的坐標;
(3)在AB下方的拋物線上是否存在點M,使∠ABO=∠ABM?若存在,求出點M到y軸的距離;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,點M到y軸的距離為
;(3)存在,點M到y軸的距離為![]()
【解析】
(1)由待定系數法可求解析式;
(2)設直線BP與x軸交于點E,過點P作PD⊥OA于D,設點P(a,![]() a2-
a2-![]() a-2),則PD=
a-2),則PD=![]() a2-
a2-![]() a-2,利用參數求出BP解析式,可求點E坐標,由三角形面積公式可求a,即可得點P坐標;
a-2,利用參數求出BP解析式,可求點E坐標,由三角形面積公式可求a,即可得點P坐標;
(3)如圖2,延長BM到N,使BN=BO,連接ON交AB于H,過點H作HF⊥AO于F,由全等三角形的性質和銳角三角函數求出點N坐標,求出BN解析式,可求點M坐標,即可求解.
(1)∵二次函數y=ax2+bx-2的圖象過點A(4,0),點C (3,-2),
∴![]() ,
,
解得: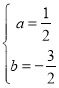
∴二次函數表達式為:![]() ;
;
(2)設直線BP與x軸交于點E,過點P作PD⊥OA于D,

設點P(a,![]() a2-
a2-![]() a-2),則PD=
a-2),則PD=![]() a2-
a2-![]() a-2,
a-2,
∵二次函數![]() 與y軸交于點B,
與y軸交于點B,
∴點B(0,-2),
設BP解析式為:![]() ,
,
∴![]() a2-
a2-![]() a-2=ka﹣2,
a-2=ka﹣2,
∴![]() ,
,
∴BP解析式為:y=(![]() )x﹣2,
)x﹣2,
∴y=0時,![]() ,
,
∴點E(![]() ,0),
,0),
∵S△PBA=5,
∵S△PBA=![]() ,
,
∴![]() ,
,
∴a=-1(不合題意舍去),a=5,
∴點P(5,3);
(3)如圖2,延長BM到N,使BN=BO,連接ON交AB于H,過點H作HF⊥AO于F,
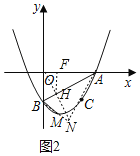
∵BN=BO,∠ABO=∠ABM,AB=AB,
∴△ABO≌△ABN(SAS)
∴AO=AN,且BN=BO,
∴AB垂直平分ON,
∴OH=HN,AB⊥ON,
∵AO=4,BO=2,
∴AB=![]() ,
,
∵S△AOB=![]() ×OA×OB=
×OA×OB=![]() ×AB×OH,
×AB×OH,
∴OH=![]() ,
,
∴AH= ,
,
∵cos∠BAO=![]() ,
,
∴ ,
,
∴AF=![]() ,
,
∴HF=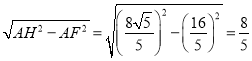 ,
,
OF=AO﹣AF= 4﹣![]() =
=![]() ,
,
∴點H(![]() ,-
,-![]() ),
),
∵OH=HN,
∴點N(![]() ,﹣
,﹣![]() )
)
設直線BN解析式為:y=mx﹣2,
∴﹣![]() =
=![]() m﹣2,
m﹣2,
∴m=﹣![]() ,
,
∴直線BN解析式為:y=﹣![]() x﹣2,
x﹣2,
∴![]() x2﹣
x2﹣![]() x﹣2=﹣
x﹣2=﹣![]() x﹣2,
x﹣2,
∴x=0(不合題意舍去),x=![]() ,
,
∴點M坐標(![]() ,﹣
,﹣![]() ),
),
∴點M到y軸的距離為![]() .
.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】關于二次函數y=x2+2x+3的圖象有以下說法:其中正確的個數是( )
①它開口向下;②它的對稱軸是過點(﹣1,3)且平行于y軸的直線;③它與x軸沒有公共點;④它與y軸的交點坐標為(3,0).
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
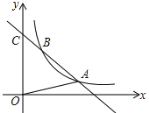
【題目】如圖,一次函數的圖象與y軸交于C(0,8),且與反比例函數y=![]() (x>0)的圖象在第一象限內交于A(3,a),B(1,b)兩點.
(x>0)的圖象在第一象限內交于A(3,a),B(1,b)兩點.
⑴求△AOC的面積;
⑵若![]() =4,求反比例函數和一次函數的解析式.
=4,求反比例函數和一次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,BC∥AD,BC=![]() AD,點E為AD的中點,點F為AE的中點,AC⊥CD,連接BE、CE、CF.
AD,點E為AD的中點,點F為AE的中點,AC⊥CD,連接BE、CE、CF.
(1)判斷四邊形ABCE的形狀,并說明理由;
(2)如果AB=4,∠D=30°,點P為BE上的動點,求△PAF的周長的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
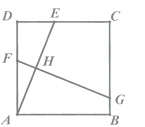
【題目】如圖,在正方形ABCD中,AD=6,點E是邊CD上的動點(點E不與端點C,D重合),AE的垂直平分線FG分別交AD,AE,BC于點F,H,G.當![]() =
=![]() 時,DE的長為( )
時,DE的長為( )
A. 2 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館有若干間標準房,當標準房的價格為![]() 元時,每天入住的國間數為
元時,每天入住的國間數為![]() 間,經市場調查表明,該賓館每間標準房的價格在
間,經市場調查表明,該賓館每間標準房的價格在![]() 元之間(含
元之間(含![]() 元,
元,![]() 元)浮動時,每天人住的房間數
元)浮動時,每天人住的房間數![]() (間)與每間標準房的價格
(間)與每間標準房的價格![]() (元)的數據如下表:
(元)的數據如下表:
| …… | 190 | 200 | 210 | 220 | …… |
| …… | 65 | 60 | 55 | 50 | …… |
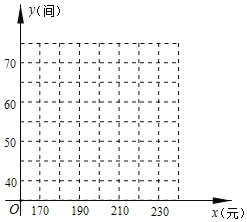
(1)根據所給數據在坐標系中描出相應的點,并畫出圖象.
(2)猜想(1)中的圖象是什么函數的圖象,求![]() 關于
關于![]() 的函數表達式,并寫出自變量
的函數表達式,并寫出自變量![]() 的取值范圍.
的取值范圍.
(3)設客房的日營業額為W (元).若不考慮其他因素,問賓館標準房的價格定為多少元時,客房的日營業額最大?最大為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平行四邊形ABCD中,對角線AC,BD交于點O,E是邊AD上的一個動點(與點A,D不重合),連接EO并延長,交BC于點F,連接BE,DF.下列說法:
① 對于任意的點E,四邊形BEDF都是平行四邊形;
② 當∠ABC>90°時,至少存在一個點E,使得四邊形BEDF是矩形;
③ 當AB<AD時,至少存在一個點E,使得是四邊形BEDF是菱形;
④ 當∠ADB=45°時,至少存在一個點E,使得是四邊形BEDF是正方形.
所有正確說法的序號是:_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠BAD=100°,∠B=∠D=90°,在BC、CD上分別找一個點M、N,使△AMN的周長最小,則∠AMN+∠ANM的度數為( )

A.130°B.120°C.160°D.100°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠ABC=60°,E是對角線AC上一點.F是線段BC延長線上一點,且CF=AE連接BE

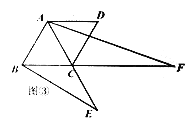
(1)發現問題:如圖①,若E是線段AC的中點,連接EF,其他條件不變,猜想線段BE與EF的數量關系
(2)探究問題:如圖②,若E是線段AC上任意一點,連接EF,其他條件不變,猜想線段BE與EF的數量關系是什么?請證明你的猜想
(3)解決問題:如圖③,若E是線段AC延長線上任意一點,其他條件不變,且∠EBC=30°,AB=3請直接寫出AF的長度
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com