
【題目】如圖是拋物線型拱橋,當拱頂離水面2m時,水面寬4m,水面下降2m,水面寬度增加______m.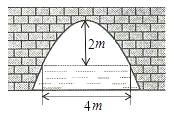
【答案】4![]() -4
-4
【解析】
根據已知建立平面直角坐標系,進而求出二次函數解析式,再通過把![]() 代入拋物線解析式得出水面寬度,即可得出答案.
代入拋物線解析式得出水面寬度,即可得出答案.
建立平面直角坐標系,設橫軸x通過AB,縱軸y通過AB中點O且通過C點,則通過畫圖可得知O為原點,
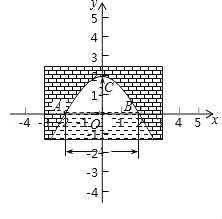
拋物線以y軸為對稱軸,且經過A,B兩點,OA和OB可求出為AB的一半2米,拋物線頂點C坐標為![]()
通過以上條件可設頂點式![]() ,其中
,其中![]() 可通過代入A點坐標
可通過代入A點坐標![]()
代入到拋物線解析式得出:![]() 所以拋物線解析式為
所以拋物線解析式為![]()
當水面下降2米,通過拋物線在圖上的觀察可轉化為:
當![]() 時,對應的拋物線上兩點之間的距離,也就是直線
時,對應的拋物線上兩點之間的距離,也就是直線![]() 與拋物線相交的兩點之間的距離,
與拋物線相交的兩點之間的距離,
可以通過把![]() 代入拋物線解析式得出:
代入拋物線解析式得出:
![]() 解得:
解得:![]()
所以水面寬度增加到![]() 米,比原先的寬度當然是增加了
米,比原先的寬度當然是增加了![]()
故答案是: ![]()


科目:初中數學 來源: 題型:
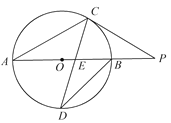
【題目】已知:AB為⊙O的直徑,延長AB到點P,過點P作圓O的切線,切點為C,連接AC,且AC=CP.
(1)求∠P的度數;
(2)若點D是弧AB的中點,連接CD交AB于點E,且DE·DC=20,求⊙O的面積.(π取3.14)
查看答案和解析>>
科目:初中數學 來源: 題型:
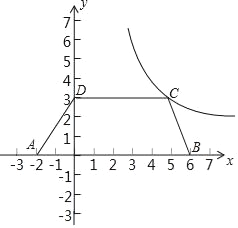
【題目】如圖,在四邊形ABCD中,CD∥AB,AD=BC.已知A(﹣2,0),B(6,0),D(0,3),函數y=![]() (x>0)的圖象G經過點C.
(x>0)的圖象G經過點C.
(1)求點C的坐標和函數y=![]() (x>0)的表達式;
(x>0)的表達式;
(2)將四邊形ABCD向上平移2個單位得到四邊形A'B'C'D',問點B'是否落在圖象G上?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】京劇臉譜是京劇藝術獨特的表現形式.京劇表演中,經常用臉譜象征人物的性格,品質,甚至角色和命運.如紅臉代表忠心耿直,黑臉代表強悍勇猛.現有三張不透明的卡片,其中兩張卡片的正面圖案為“紅臉”,另外一張卡片的正面圖案為“黑臉”,卡片除正面圖案不同外,其余均相同,將這三張卡片背面向上洗勻,從中隨機抽取一張,記錄圖案后放回,重新洗勻后再從中隨機抽取一張.
請用畫樹狀圖或列表的方法,求抽出的兩張卡片上的圖案都是“紅臉”的概率.(圖案為“紅臉”的兩張卡片分別記為A1、A2,圖案為“黑臉”的卡片記為B)

查看答案和解析>>
科目:初中數學 來源: 題型:
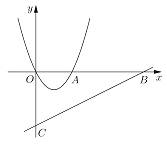
【題目】如圖,已知,二次函數![]() 的圖像交
的圖像交![]() 軸正半軸于點
軸正半軸于點![]() ,頂點為
,頂點為![]() ,一次函數
,一次函數![]() 的圖像交
的圖像交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,
,![]() 的正切值為
的正切值為![]() .
.
(1)求二次函數的解析式與頂點![]() 坐標;
坐標;
(2)將二次函數圖像向下平移![]() 個單位,設平移后拋物線頂點為
個單位,設平移后拋物線頂點為![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() (k>0)的圖像交于A,B兩點,過點A做x軸的垂線,垂足為M,△AOM面積為1.
(k>0)的圖像交于A,B兩點,過點A做x軸的垂線,垂足為M,△AOM面積為1.
(1)求反比例函數的解析式;
(2)在y軸上求一點P,使PA+PB的值最小,并求出其最小值和P點坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
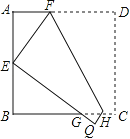
【題目】如圖,將邊長為6cm的正方形ABCD折疊,使點D落在AB邊的中點E處,折痕為FH,點C落在Q處,EQ與BC交于點G,則△EBG的周長是 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
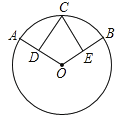
【題目】如圖,D、E分別是⊙O兩條半徑OA、OB的中點,![]() .
.
(1)求證:CD=CE.
(2)若∠AOB=120°,OA=x,四邊形ODCE的面積為y,求y與x的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以點B為旋轉中心,將△ABC沿逆時針方向旋轉90°得到△A′BC′,請畫出變換后的圖形;
(2)求點A和點A′之間的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com