
【題目】如圖,四邊形ABCD是菱形,對角線AC=16cm,BD=12cm,DH⊥BC于點H,交AC于點G.
(1)寫出兩個不全等且與△GHC相似的三角形,并任選其中的一個進行證明;
(2)求GH的長.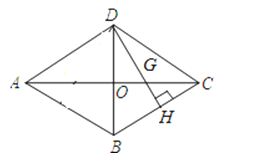
【答案】解:(1)△BOC∽△GHC,△GDO∽△GHC,
理由如下:
∵四邊形ABCD是菱形,
∴BD⊥CD,
∴∠DOG=90°,
∵DH⊥BC于點H,
∴∠GHC=90°,
∵∠DGO=∠CGH,
∴△GDO∽△GHC;
(2)在菱形ABCD中,AC⊥BD,
∵AC=24cm,BD=18cm,
∴OA=![]() AC=
AC=![]() ×16=8,OB=
×16=8,OB=![]() BD=
BD=![]() ×12=6cm,
×12=6cm,
在Rt△AOB中,AB=10cm,
∵DH⊥AB,
∴菱形ABCD的面積=![]() ACBD=ABDH,
ACBD=ABDH,
即![]() ×16×12=10DH,
×16×12=10DH,
解得DH=9.6(cm).
在Rt△DHB中,BH═7.2cm,
則AH=AB﹣BH=10﹣7.2=2.8(cm),
∵tan∠HAG=![]() =
=![]() =
=![]() ,
,
∴GH=![]() AH=2.1(cm).
AH=2.1(cm).
【解析】(1)根據菱形的性質以及相似三角形的判定方法即可得到和GHC相似的三角形;
(2)根據菱形的對角線互相垂直平分求出OA、OB,再根據勾股定理列式求出AB,然后利用菱形的面積列式計算即可得DH的長,在Rt△DHB中求出BH,然后得出AH,利用tan∠HAG的值,可得出GH的值.
【考點精析】認真審題,首先需要了解菱形的性質(菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半).


 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.成中心對稱的兩個圖形全等
B.全等的兩個圖形成中心對稱
C.成中心對稱的兩個圖形一定關于某條直線對稱
D.關于某條直線成軸對稱的兩個圖形一定關于某一點成中心對稱
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E、F是四邊形ABCD的對角線AC上兩點,AE=CF,DF∥BE,DF=BE.
(1)求證:四邊形ABCD是平行四邊形;
(2)若AC平分∠BAD,求證:ABCD為菱形.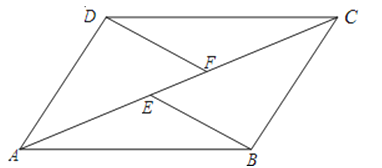
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚中華優秀傳統文化,今年2月20日舉行了襄陽市首屆中小學生經典誦讀大賽決賽. 某中學為了選拔優秀學生參加,廣泛開展校級“經典誦讀”比賽活動,比賽成績評定為A,B,C,D,E五個等級,該校七(1)班全體學生參加了學校的比賽,并將比賽結果繪制成如下兩幅不完整的統計圖.請根據圖中信息,解答下列問題:
(1)該校七(1)班共有 名學生;扇形統計圖中C等級所對應扇形的圓心角等于 度;
(2)補全條形統計圖;
(3)若A等級的4名學生中有2名男生2名女生,現從中任意選取2名參加學校培訓班,請用列表法或畫樹狀圖的方法,求出恰好選到1名男生和1名女生的概率.
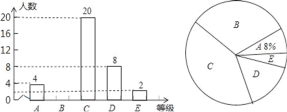
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com