
【題目】如圖所示:拋物線![]() 交坐標(biāo)軸于
交坐標(biāo)軸于![]() 、
、![]() 、
、![]() 三點,
三點,![]() 是拋物線的頂點,
是拋物線的頂點,![]() 在對稱軸上,
在對稱軸上,![]() 在坐標(biāo)軸上.以下結(jié)論:
在坐標(biāo)軸上.以下結(jié)論:
①存在點![]() ,使
,使![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() 的最小值是
的最小值是![]() ;③
;③![]() 的最大值是
的最大值是![]() ;④若
;④若![]() 與
與![]() 相似,則
相似,則![]() 的坐標(biāo)恰有兩個.
的坐標(biāo)恰有兩個.
其中正確的是________(只填序號)
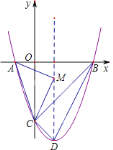
【答案】①②③
【解析】
先根據(jù)拋物線的解析式確定點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點
,點![]() 坐標(biāo)為
坐標(biāo)為![]() ,點
,點![]() 坐標(biāo)為
坐標(biāo)為![]() ,對稱軸為直線
,對稱軸為直線![]() ,
,![]() 點坐標(biāo)為
點坐標(biāo)為![]() ;由于
;由于![]() 為等腰直角三角形,易得
為等腰直角三角形,易得![]() ,則
,則![]() ,可得到
,可得到![]() 點坐標(biāo)為
點坐標(biāo)為![]() ;由于點
;由于點![]() 與點
與點![]() 關(guān)于直線
關(guān)于直線![]() 對稱,根據(jù)兩點之間線段最短得到當(dāng)
對稱,根據(jù)兩點之間線段最短得到當(dāng)![]() 點在
點在![]() 的位置時,
的位置時,![]() 有最小值,最小值為
有最小值,最小值為![]() 的長,運用勾股定理可計算
的長,運用勾股定理可計算![]() ;由于三角形任意兩邊之差小于第三邊,則當(dāng)
;由于三角形任意兩邊之差小于第三邊,則當(dāng)![]() 點在
點在![]() 的位置時,
的位置時,![]() 有最大值,最大值為
有最大值,最大值為![]() 的長,再根據(jù)勾股定理可計算出
的長,再根據(jù)勾股定理可計算出![]() ;根據(jù)勾股定理的逆定理可得到
;根據(jù)勾股定理的逆定理可得到![]() ,若
,若![]() 與
與![]() 相似,則
相似,則![]() 為直角三角形,當(dāng)
為直角三角形,當(dāng)![]() 時,根據(jù)
時,根據(jù)![]() ,可得到
,可得到![]() ,則
,則![]() 滿足條件;當(dāng)
滿足條件;當(dāng)![]() 時,由于
時,由于![]() ,可得到
,可得到![]() 滿足條件;當(dāng)
滿足條件;當(dāng)![]() 時,由于
時,由于![]() 得到
得到![]() ,則有
,則有![]() 滿足條件.
滿足條件.
令![]() ,則
,則![]() ,解得
,解得![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,
![]() 點
點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點
,點![]() 坐標(biāo)為
坐標(biāo)為![]() ,點
,點![]() 坐標(biāo)為
坐標(biāo)為![]() ,
,
![]()
![]() ,
,
![]() 拋物線的對稱軸為直線
拋物線的對稱軸為直線![]() ,
,![]() 點坐標(biāo)為
點坐標(biāo)為![]() ,
,
(1)設(shè)![]() 點坐標(biāo)為
點坐標(biāo)為![]() ,作
,作![]() 直線
直線![]() ,直線
,直線![]() 與
與![]() 軸交于
軸交于![]() 點,如圖,
點,如圖,
當(dāng)![]() 為等腰直角三角形,則
為等腰直角三角形,則![]() ,
,
![]()
![]() ,
,
![]()
![]() 點坐標(biāo)為
點坐標(biāo)為![]() ,所以①正確;
,所以①正確;
(2)點![]() 與點
與點![]() 關(guān)于直線
關(guān)于直線![]() 對稱,
對稱,![]() 與直線
與直線![]() 的交點為
的交點為![]() ,
,
當(dāng)![]() 點在
點在![]() 的位置時,
的位置時,![]() 有最小值,最小值為
有最小值,最小值為![]() 的長,即
的長,即![]() ,所以②正確;
,所以②正確;
(3)延長![]() 交直線
交直線![]() 于
于![]() ,
,
當(dāng)![]() 點在
點在![]() 的位置時,
的位置時,![]() 有最大值,最大值為
有最大值,最大值為![]() 的長,即
的長,即![]() ,所以③正確;
,所以③正確;
(3)![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
點![]() 點在原點,即
點在原點,即![]() 的位置時,
的位置時,![]() ,
,
![]()
![]() ,
,
![]()
![]() 滿足條件,
滿足條件,
當(dāng)![]() 時,
時,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() 滿足條件;
滿足條件;
當(dāng)![]() 時,
時,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() 滿足條件,所以④錯誤.
滿足條件,所以④錯誤.
故答案為:①②③.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,已知△ABC的三個頂點的坐標(biāo)分別為A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
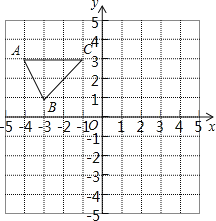
(1)請按下列要求畫圖:
①將△ABC先向右平移4個單位長度、再向上平移2個單位長度,得到△A1B1C1,畫出△A1B1C1;
②△A2B2C2與△ABC關(guān)于原點O成中心對稱,畫出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2關(guān)于點M成中心對稱,請直接寫出對稱中心M點的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,有一種動畫程序,在平面直角坐標(biāo)系屏幕上,直角三角形是黑色區(qū)域(含直角三角形邊界),其中A(1,1),B(2,1),C(1,3),用信號槍沿直線y=3x+b發(fā)射信號,當(dāng)信號遇到黑色區(qū)域時,區(qū)域便由黑變白,則能夠使黑色區(qū)域變白的b的取值范圍是( )

A.﹣5≤b≤0B.﹣5<b≤﹣3C.﹣5≤b≤3D.﹣5≤b≤5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點O是△ABC內(nèi)一點,∠A=80°,BO、CO分別是∠ABC和∠ACB的角平分線,則∠BOC等于( )

A. 140° B. 120° C. 130° D. 無法確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等腰直角![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 的平分線交于點
的平分線交于點![]() .
.

(1)求證:![]() ;
;
(2)若![]() 的外角平分線以及
的外角平分線以及![]() 的平分線交于點
的平分線交于點![]() ,(1)結(jié)論是否成立?請在圖中補(bǔ)全圖形,寫出結(jié)論,并說明理由.
,(1)結(jié)論是否成立?請在圖中補(bǔ)全圖形,寫出結(jié)論,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() (
(![]() 是常數(shù))的頂點為
是常數(shù))的頂點為![]() ,直線
,直線![]()

![]() 求證:點
求證:點![]() 在直線
在直線![]() 上;
上;
![]() 當(dāng)
當(dāng)![]() 時,拋物線與
時,拋物線與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,與直線
,與直線![]() 的另一個交點為
的另一個交點為![]() ,
,![]() 是
是![]() 軸下方拋物線上的一點,
軸下方拋物線上的一點,![]() (如圖),求點
(如圖),求點![]() 的坐標(biāo);
的坐標(biāo);
![]() 若以拋物線和直線
若以拋物線和直線![]() 的兩個交點及坐標(biāo)原點為頂點的三角形是等腰三角形,請直接寫出所有符合條件的
的兩個交點及坐標(biāo)原點為頂點的三角形是等腰三角形,請直接寫出所有符合條件的![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ ABC中,AB = AC

(1)如圖 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,則∠EDC =
(2)如圖 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,則∠EDC =
(3)思考:通過以上兩題,你發(fā)現(xiàn)∠BAD與∠EDC之間有什么關(guān)系?請用式子表示:
(4)如圖 3,如果AD不是BC上的高,AD = AE,是否仍有上述關(guān)系?如有,請你寫出來,并說明理由
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
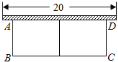
【題目】如圖,有長為![]() 的籬笆,一面利用墻(墻的最大可用長度為
的籬笆,一面利用墻(墻的最大可用長度為![]() ),圍成中間隔有一道籬笆(平行于
),圍成中間隔有一道籬笆(平行于![]() )的矩形花圃
)的矩形花圃![]() .設(shè)花圃的一邊
.設(shè)花圃的一邊![]() 為
為![]() .
.
![]() 則
則![]() ________(用含
________(用含![]() 的代數(shù)式表示),矩形
的代數(shù)式表示),矩形![]() 的面積
的面積![]() ________(用含
________(用含![]() 的代數(shù)式表示);
的代數(shù)式表示);
![]() 如果要圍成面積為
如果要圍成面積為![]() 的花圃,
的花圃,![]() 的長是多少?
的長是多少?
![]() 將
將![]() 中表示矩形
中表示矩形![]() 的面積的代數(shù)式通過配方,問:當(dāng)
的面積的代數(shù)式通過配方,問:當(dāng)![]() 等于多少時,能夠使矩形花圃
等于多少時,能夠使矩形花圃![]() 面積最大,最大的面積為多少?
面積最大,最大的面積為多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知等腰△ABC的底邊BC=20cm,D是腰AB上一點,且CD=16cm,BD=12cm,

(1)求△ABC中BC邊上的高
(2)求△ABC的周長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com