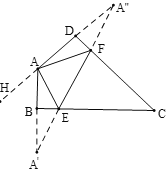
【題目】在四邊形ABCD中∠C＝55°，∠B＝∠D＝90°，E，F分別是BC，DC上的點，當△EAF周長最小時，∠EAF的度數為（ ）
A.55°B.70°C.125°D.110°
【答案】B
【解析】
作點A關于BC和CD的對稱點A′，A″，連接A′A″，交BC于E，交CD于F，作DA延長線AH，根據三角形的三邊在同一直線上可得△AEF的周長最小值．根據四邊形內角和可求出∠DAB=125°，根據外角性質可得∠A′+∠A″＝∠HAA′＝55°，根據軸對稱的性質可得∠A′＝∠EAA′，∠FAD＝∠A″，根據∠DAB=∠EAA′+∠FAD+∠EAF即可求出∠EAF的度數.
作A關于BC和CD的對稱點A′，A″，連接A′A″，交BC于E，交CD于F，作DA延長線AH，
∵點A′，A″是點A關于BC和CD的對稱點，
∴AE=A′E，AF=A″F，
∴∠A′＝∠EAA′，∠FAD＝∠A″，A′A″即為△AEF的周長最小值．
∵∠C＝55°，∠ABC＝∠ADC＝90°，
∴∠DAB＝125°，
∴∠HAA′＝55°，
∴∠A′+∠A″＝∠HAA′＝55°，
∴∠EAA′+∠A″AF＝55°，
∴∠EAF＝125°﹣55°＝70°．
故選B．
金鑰匙試卷系列答案科目：初中數學 來源： 題型：
【題目】一列快車從甲地勻速駛往乙地，一列慢車從乙地勻速駛往甲地．設先發車輛行駛的時間為xh，兩車之間的距離為ykm，圖中的折線表示y與x之間的函數關系，根據圖象解決以下問題：
（1）慢車的速度為_____km/h，快車的速度為_____km/h；
（2）解釋圖中點C的實際意義并求出點C的坐標；
（3）求當x為多少時，兩車之間的距離為500km．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝BC，∠ABC＝90°，BM是AC邊上的中線，點D，E分別在邊AC和BC上，DB＝DE，DE與BM相交于點N，EF⊥AC于點F，以下結論：
①∠DBM＝∠CDE；②S△BDE<S四邊形BMFE；③CD·EN＝BN·BD；④AC＝2DF.
其中正確結論的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1,在平面直角坐標系中,A(5， 0), B(0， 5), C(2， 0),連AB
(1)如圖2，D為第一象限內一點，CD
BC于點C,ADAB于點A,求點D坐標；
(2)E為
軸負半軸上一動點，連BE，在軸下方做EFBE于點E，并且EF=BE,連FC，直接寫出當CF最短時點E的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某人在山坡坡腳C處測得一座建筑物頂點A的仰角為63.4°，沿山坡向上走到P處再測得該建筑物頂點A的仰角為53°．已知BC=90米，且B、C、D在同一條直線上，山坡坡度i=5:12.
（1）求此人所在位置點P的鉛直高度．（結果精確到0.1米）
（2）求此人從所在位置點P走到建筑物底部B點的路程（結果精確到0.1米）
（測傾器的高度忽略不計，參考數據：tan53°≈
，tan63.5°≈2）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）觀察推理：如圖1，△ABC中，∠ACB＝90°，AC＝BC，直線l過點C，點A，B在直線l同側，BD⊥l，AE⊥l，垂足分別為D，E．求證：△AEC≌△CDB；
（2）類比探究：如圖2，Rt△ABC中，∠ACB＝90°，AC＝2，將斜邊AB繞點A逆時針旋轉90°至AB'，連接B′C，求△AB′C的面積.
（3）拓展提升：如圖3，等邊△EBC中，EC＝BC＝3cm，點O在BC上且OC＝2cm，動點P從點E沿射線EC以lcm/s速度運動，連接OP，將線段OP繞點O逆時針旋轉120°得到線段OF，設點P運動的時間為t秒．
①當t＝______秒時，OF∥ED.
②當t＝______秒時，點F恰好落在射線EB上．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AO⊥OM，OA＝6cm，點B為射線OM上的一個動點，分別以OB、AB為直角邊，點B為直角頂點，在OM兩側作等腰Rt△OBF、等腰Rt△ABE，連接EF交OM于P點，當點B在射線OM上移動時，PB的長度是_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com