
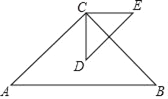
【題目】已知:如圖,點D是等腰直角△ABC的重心,其中∠ACB=90°,將線段CD繞點C逆時針旋轉90°得到線段CE,連結DE,若△ABC的周長為6,則△DCE的周長為( )
A. 2![]() B. 2
B. 2![]() C. 4 D. 3
C. 4 D. 3![]()
【答案】A
【解析】
延長CD交AB于F.如圖,利用等腰直角三角形的性質和重心的性質得到CF平分AB,CD=2DF,則CF=![]() AB=
AB=![]() CA,所以CD=
CA,所以CD=![]() CA,再利用旋轉的性質可判斷△CDE為等腰直角三角形,于是可判定△CDE∽△CAB,然后根據相似三角形的性質計算△CDE的周長.
CA,再利用旋轉的性質可判斷△CDE為等腰直角三角形,于是可判定△CDE∽△CAB,然后根據相似三角形的性質計算△CDE的周長.
解:延長CD交AB于F.如圖,
∵點D是等腰直角△ABC的重心,
∴CF平分AB,CD=2DF,
∴CF=![]() AB=
AB=![]()
![]() CA=
CA=![]() CA,
CA,
∴CD=![]() CF=
CF=![]() CA,
CA,
∵線段CD繞點C逆時針旋轉90°得到線段CE,
∴CD=CE,∠DCE=90°,
∴△CDE為等腰直角三角形,
∴△CDE∽△CAB,
∴△CDE的周長:△CAB的周長=CD:CA=![]() ,
,
∴△CDE的周長=![]() ×6=2
×6=2![]() .
.
故選:A.


科目:初中數學 來源: 題型:
【題目】綜合與實踐:
觀察發現:①![]() ;
;
②![]() ;
;
③![]() ;
;
…
解決問題:
(1)利用你觀察到的規律,化簡![]() ;
;
(2)計算:![]() .
.
拓廣探索:
定義:如果兩個含有二次根式的非零代數式相乘,它們的積不含有二次根式,就說這兩個非零代數式互為有理化因式.例如,上面計算中![]() 和
和![]() 、
、![]() 和
和![]() 等都是互為有理化因式.通過上面的觀察,我們還可以發現:如果二次根式的分母原來為無理數,那么把分子、分母同乘以分母的互為有理化因式,可以將該二次根式的分母化為有理數.
等都是互為有理化因式.通過上面的觀察,我們還可以發現:如果二次根式的分母原來為無理數,那么把分子、分母同乘以分母的互為有理化因式,可以將該二次根式的分母化為有理數.
(3)根據閱讀,將![]() 的分母化為有理數.
的分母化為有理數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]()
(1)求證:無論![]() 取何實數值,方程總有實數根;
取何實數值,方程總有實數根;
(2)若等腰三角形![]() 的一邊長
的一邊長![]() ,另兩邊長
,另兩邊長![]() 、
、![]() 恰好是這個方程的兩個根,求此三角形的周長
恰好是這個方程的兩個根,求此三角形的周長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2﹣2x+3與x軸交于A、B兩點,與y軸交于C點,M點在拋物線的對稱軸上,當點M到點B的距離與到點C的距離之和最小時,點M的坐標為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了編撰祖國的優秀傳統文化,某校組織了一次“詩詞大會”,小明和小麗同時參加,其中,有一道必答題是:從如圖所示的九宮格中選取七個字組成一句唐詩,其答案為“山重水復疑無路”.
(1)小明回答該問題時,對第二個字是選“重”還是選“窮”難以抉擇,若隨機選擇其中一個,則小明回答正確的概率是 ;
(2)小麗回答該問題時,對第二個字是選“重”還是選“窮”、第四個字是選“富”還是選“復”都難以抉擇,若分別隨機選擇,請用列表或畫樹狀圖的方法求小麗回答正確的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】爸爸想送小明一個書包和一輛自行車作為新年禮物,在甲、乙兩商場都發現同款的自行車單價相同,書包單價也相同,自行車和書包單價之和為452元,且自行車的單價比書包的單價4倍少8元.
(1)求自行車和書包單價各為多少元;
(2)新年來臨趕上商家促銷,乙商場所有商品打八五折(即8.5折)銷售,甲全場購物毎滿100元返購物券30元(即不足100元不返券,滿100元送30元購物券,滿200元送60元購物券),并可當場用于購物,購物券全場通用.但爸爸只帶了400元錢,如果他只在同一家商場購買看中的兩樣物品,在哪一家買更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【新知理解】
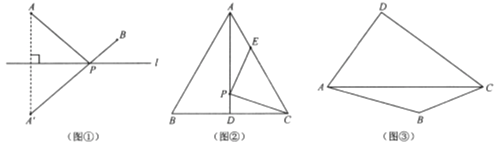
如圖①,若點![]() 、
、![]() 在直線l同側,在直線l上找一點
在直線l同側,在直線l上找一點![]() ,使
,使![]() 的值最小.
的值最小.
作法:作點![]() 關于直線l的對稱點
關于直線l的對稱點![]() ,連接
,連接![]() 交直線l于點
交直線l于點![]() ,則點
,則點![]() 即為所求.
即為所求.
【解決問題】
如圖②,![]() 是邊長為6cm的等邊三角形
是邊長為6cm的等邊三角形![]() 的中線,點
的中線,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,則
上,則![]() 的最小值為 cm;
的最小值為 cm;
【拓展研究】
如圖③,在四邊形![]() 的對角線
的對角線![]() 上找一點
上找一點![]() ,使
,使![]() .(保留作圖痕跡,并對作圖方法進行說明)
.(保留作圖痕跡,并對作圖方法進行說明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】情境![]() :小芳離開家去學校上學,走了一段路后,發現自己作業本忘家里了,于是返回家里找到作業本,然后又趕快去學校;
:小芳離開家去學校上學,走了一段路后,發現自己作業本忘家里了,于是返回家里找到作業本,然后又趕快去學校;
情境![]() :小明從家出發去圖書館還書,走了一段路程后,發現時間有點緊張,便以更快的速度前進.
:小明從家出發去圖書館還書,走了一段路程后,發現時間有點緊張,便以更快的速度前進.

(1)情境![]() 所對應的函數圖象分別是_______,_______(填寫序號);
所對應的函數圖象分別是_______,_______(填寫序號);
(2)請你為剩下的函數圖象寫出一個適合的情景.
查看答案和解析>>
科目:初中數學 來源: 題型:
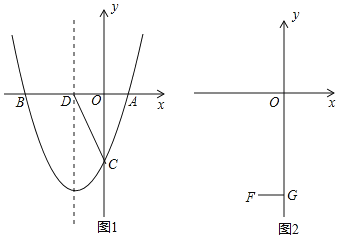
【題目】拋物線y=x2+bx+c與x軸交于A(1,0),B(m,0),與y軸交于C.
(1)若m=-3,求拋物線的解析式,并寫出拋物線的對稱軸;
(2)如圖1,在(1)的條件下,設拋物線的對稱軸交x軸于D,在拋物線對稱軸左側上有 一點E,使S△ACE=S△ACD,求E點的坐標;
(3) 如圖2,設F(-1,-4),FG⊥y軸于G,在線段OG上是否存在點P,使 ∠OBP=∠FPG? 若存在,求m的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com