
【題目】對于不等式組 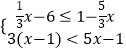 ,下列說法正確的是( )
,下列說法正確的是( )
A.此不等式組的正整數解為1,2,3
B.此不等式組的解集為﹣1<x≤ ![]()
C.此不等式組有5個整數解
D.此不等式組無解
【答案】A
【解析】解: 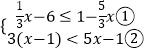 ,
,
解①得x≤ ![]() ,
,
解②得x>﹣1,
所以不等式組的解集為﹣1<x≤ ![]() ,
,
所以不等式組的正整數解為1,2,3
所以答案是:A.
【考點精析】關于本題考查的一元一次不等式組的解法和一元一次不等式組的整數解,需要了解解法:①分別求出這個不等式組中各個不等式的解集;②利用數軸表示出各個不等式的解集;③找出公共部分;④用不等式表示出這個不等式組的解集.如果這些不等式的解集的沒有公共部分,則這個不等式組無解 ( 此時也稱這個不等式組的解集為空集 );使不等式組中的每個不等式都成立的未知數的值叫不等式組的解,一個不等式組的所有的解組成的集合,叫這個不等式組的解集(簡稱不等式組的解)才能得出正確答案.


 每課必練系列答案
每課必練系列答案科目:初中數學 來源: 題型:
【題目】為了解我市的空氣質量情況,某環保興趣小組從環境監測網隨機抽取了若干天的空氣質量情況作為樣本進行統計,繪制了如圖所示的條形統計圖和扇形統計圖(部分信息未給出).

請你根據圖中提供的信息,解答下列問題:
(1)請補全條形統計圖,并求扇形統計圖中表示“重度污染”的扇形的圓心角度數;
(2)所抽取若干天的空氣質量情況的眾數是 中位數是 .
(3)請估計該市這一年(365天)達到“優”和“良”的總天數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】[知識生成]通常,用兩種不同的方法計算同一個圖形的面積,可以得到一個恒等式.例如:如圖①是一個長為![]() ,寬為
,寬為![]() 的長方形,沿圖中虛線用剪刀均分成四個小長方形,然后按圖②的形狀拼成一個正方形.請解答下列問題:
的長方形,沿圖中虛線用剪刀均分成四個小長方形,然后按圖②的形狀拼成一個正方形.請解答下列問題:
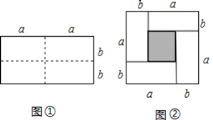
(1)圖②中陰影部分的正方形的邊長是________________;
(2)請用兩種不同的方法求圖②中陰影部分的面積:
方法1:________________________;方法2:_______________________;
(3)觀察圖②,請你寫出![]() 、
、![]() 、
、![]() 之間的等量關系是__________;
之間的等量關系是__________;
(4)根據(3)中的等量關系解決如下問題:若![]() ,
,![]() ,則
,則![]() =________;
=________;
[知識遷移]
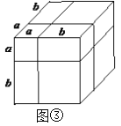
類似地,用兩種不同的方法計算同一幾何體的體積,也可以得到一個恒等式.
(5)根據圖③,寫出一個代數恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的規律求
,利用上面的規律求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點O是AC的中點,AC=2AB,延長AB至G,使BG=AB,連接GO交BC于E,延長GO交AD于F,連接AE.
求證:(1)△ABC≌△AOG;
(2)猜測四邊形AECF的形狀并證明你的猜想.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 點A1在AD邊上,A1B1與BD交于點E,D1B1與CD交于點F.
(1)求證:四邊形EB1FD是平行四邊形;
(2)若AB=3,BC=4,AA1=1,求B1F的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC為等腰直角三角形,∠ACB=90°,CD是斜邊AB上的中線,且CD=2,點E是線段BD上任意一點,以CE為邊向左側作正方形CEFG,EF交BC于點M,連接BG交EF于點N.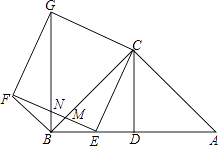
(1)證明:△CAE≌△CBG;
(2)設DE=x,BN=y,求y關于x的函數關系式,并求出y的最大值;
(3)當DE=2 ![]() ﹣2時,求∠BFE的度數.
﹣2時,求∠BFE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=2x+4
(1)在如圖所示的平面直角坐標系中,畫出函數的圖象;

2)求圖象與x軸的交點A的坐標,與y軸交點B的坐標;
(3)在(2)的條件下,求出△AOB的面積;
(4)利用圖象直接寫出:當y<0時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:![]() ,OB、OC、OM、ON是
,OB、OC、OM、ON是![]() 內的射線.
內的射線.
![]() 如圖1,若OM平分
如圖1,若OM平分![]() ,ON平分
,ON平分![]() 當OB繞點O在
當OB繞點O在![]() 內旋轉時,則
內旋轉時,則![]() 的大小為______;
的大小為______;
![]() 如圖2,若
如圖2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() 當
當![]() 繞點O在
繞點O在![]() 內旋轉時,求
內旋轉時,求![]() 的大小;
的大小;
![]() 在
在![]() 的條件下,若
的條件下,若![]() ,當
,當![]() 在
在![]() 內繞著點O以
內繞著點O以![]() 秒的速度逆時針旋轉t秒時,
秒的速度逆時針旋轉t秒時,![]() 和
和![]() 中的一個角的度數恰好是另一個角的度數的兩倍,求t的值
中的一個角的度數恰好是另一個角的度數的兩倍,求t的值

查看答案和解析>>
科目:初中數學 來源: 題型:
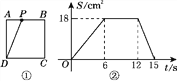
【題目】如圖①所示,正方形ABCD的邊長為6 cm,動點P從點A出發,在正方形的邊上沿A→B→C→D運動,設運動的時間為t(s),三角形APD的面積為S(cm2),S與t的函數圖象如圖②所示,請回答下列問題:
(1)點P在AB上運動的時間為________s,在CD上運動的速度為________cm/s,三角形APD的面積S的最大值為________cm2;
(2)求出點P在CD上運動時S與t之間的函數表達式;
(3)當t為何值時,三角形APD的面積為10 cm2?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com