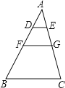
【題目】如圖，
中，
，且
，則
________．
【答案】
【解析】
由DE∥FG∥BC，平行于三角形的一邊的直線與其他兩邊相交，所構成的三角形與原三角形相似，即可判定△ADE∽△AFG∽△ABC，根據相似三角形的面積比等于相似比的平方，即可求得
，
，設S△ADE=4x，即可求得S梯形DFGE與S梯形FBCG的值，繼而求得S△ADE：S梯形DFGE：S梯形FBCG的值．
∵△ABC中，DE∥FG∥BC，
∴△ADE∽△AFG∽△ABC，
∴
，
∵AD：DF：FB=2：3：4，
∴
，
，
∴，，
設S△ADE=4x，則S△AFG=25x，S△ABC=81x，
∴S梯形DFGE=25x-4x=21x，S梯形FBCG=81x-25x=56x，
∴S△ADE：S梯形DFGE：S梯形FBCG=4：21：56．
故答案為：4：21：56．
黎明文化寒假作業系列答案科目：初中數學 來源： 題型：
【題目】八年級（1）班從學校出發去某景點旅游，全班分成甲、乙兩組，甲組乘坐大型客車，乙組乘坐小型客車．已知甲組比乙組先出發，汽車行駛的路程
(單位:
)和行駛時間
(單位:
)之間的函數關系如圖所示．
根據圖象信息，回答下列問題：
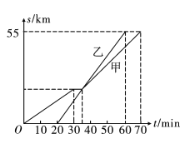
（1）學校到景點的路程為_ ，甲組比乙組先出發 ， 組先到達旅游景點；
（2）求乙組乘坐的小型客車的平均速度；
（3）從圖象中你還能獲得哪些信息？ (請寫出一條)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，BC為⊙O的切線，D為⊙O上的一點，CD=CB，延長CD交BA的延長線于點E．
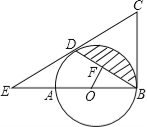
（1）求證：CD為⊙O的切線；
（2）若BD的弦心距OF=1，∠ABD=30°，求圖中陰影部分的面積．（結果保留π）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是( )
A. 各有一個角是
的兩個等腰三角形相似 B. 各有一個角是
的兩個等腰三角形相似
C. 有兩邊對應成比例的兩個等腰三角形相似 D. 兩腰對應成比例的兩個等腰三角形相似
查看答案和解析>>
科目：初中數學 來源： 題型：
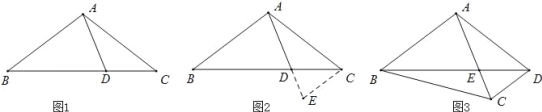
【題目】閱讀下面材料：小騰遇到這樣一個問題：如圖1，在△ABC中，點D在線段BC上，∠BAD=75°，∠CAD=30°，AD=2，BD=2DC，求AC的長．
小騰發現，過點C作CE∥AB，交AD的延長線于點E，通過構造△ACE，經過推理和計算能夠使問題得到解決（如圖 2）．
請回答：∠ACE的度數為 ，AC的長為 ．
參考小騰思考問題的方法，解決問題：
如圖 3，在四邊形 ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC與BD交于點E，AE=2，BE=2ED，求BC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在邊長為1的小正方形網格中，△AOB的頂點均在格點上．
（1）B點關于y軸的對稱點坐標為 ；
（2）將△AOB向左平移3個單位長度得到△A1O1B1，請畫出△A1O1B1；
（3）在（2）的條件下，A1的坐標為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，∠A=30°，以AB為直徑的⊙O交BC于點D，交AC于點E，連結DE，過點B作BP平行于DE，交⊙O于點P，連結EP、CP、OP．
（1）BD=DC嗎？說明理由；
（2）求∠BOP的度數；
（3）求證：CP是⊙O的切線．
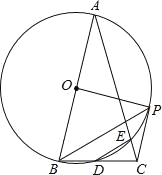
查看答案和解析>>
科目：初中數學 來源： 題型：
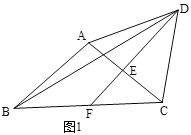
【題目】在△ABC中，AB=AC，在△ABC的外部作等邊三角形△ACD，E為AC的中點，連接DE并延長交BC于點F，連接BD．
（1）如圖1，若∠BAC=100°，則∠ABD的度數為_____，∠BDF的度數為______；
（2）如圖2，∠ACB的平分線交AB于點M，交EF于點N，連接BN，若BN=DN，∠ACB=
．
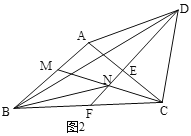
(I)用表示∠BAD；
(II)①求證：∠ABN=30°；
②直接寫出的度數以及△BMN的形狀．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
