
 如圖,在正方形ABCD中,AB=4,E,F分別是邊BC,CD邊上的動點,且AE=AF,設△AEF的面積為y,EC的長為x.
如圖,在正方形ABCD中,AB=4,E,F分別是邊BC,CD邊上的動點,且AE=AF,設△AEF的面積為y,EC的長為x.分析 (1)根據正方形的性質可得AB=AD,再利用“HL”證明Rt△ABE和Rt△ADF全等,根據全等三角形對應邊相等可得BE=DF,然后求出CE=CF,再根據△AEF的面積等于正方形的面積減去三個直角三角形的面積列式整理即可得解;
(2)結合(1)中二次函數解析式和x的取值范圍來求△AEF的面積的最大值;
(3)利用(1)中二次函數解析式畫出函數圖象,注意x的取值范圍.
解答 解:(1)在正方形ABCD中,AB=AD,
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,
∵CE=x,
∴BE=DF=4-x,
∴y=42-2×$\frac{1}{2}$×4×(4-x)-$\frac{1}{2}$x2,
=-$\frac{1}{2}$x2+4x,
即y=-$\frac{1}{2}$x2+4x.
∵E、F分別是BC、CD邊上的動點,且保證A、E、F能構成三角形,
∴x的取值范圍是:0≤x≤4;
(2)∵y=-$\frac{1}{2}$x2+4x=-$\frac{1}{2}$(x-4)2+8,0<x≤4,
∴當x=4時,△AEF的面積最大,最大面積是8;
(3)如圖所示,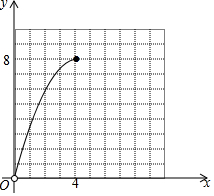
點評 本題考查了四邊形綜合題,涉及到了正方形的性質,全等三角形的判定與性質,三角形的面積以及二次函數最值的求法和二次函數圖象,熟記性質并求出三角形全等是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | x1=1,x2=2 | B. | x1=-1,x2=2 | C. | x1=1,x2=-2 | D. | x1=-1,x2=-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
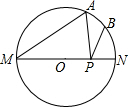 如圖,MN是⊙O的直徑,MN=4,∠AMN=30°,點B為弧AN的中點,點P是直徑MN上的一個動點,則PA+PB的最小值為( )
如圖,MN是⊙O的直徑,MN=4,∠AMN=30°,點B為弧AN的中點,點P是直徑MN上的一個動點,則PA+PB的最小值為( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
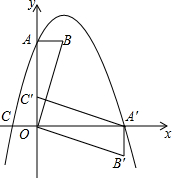 在平面直角坐標系中,平行四邊形ABOC如圖放置,點A、C的坐標分別是(0,4)、(-1,0),將此平行四邊形繞點O順時針旋轉90°,得到平行四邊形A′B′OC′.
在平面直角坐標系中,平行四邊形ABOC如圖放置,點A、C的坐標分別是(0,4)、(-1,0),將此平行四邊形繞點O順時針旋轉90°,得到平行四邊形A′B′OC′.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com