
如圖,在平面直角坐標系中,點M是第一象限內一點,過M的直線分別交 軸,
軸, 軸的正半軸于A,B兩點,且M是AB的中點. 以OM為直徑的⊙P分別交
軸的正半軸于A,B兩點,且M是AB的中點. 以OM為直徑的⊙P分別交 軸,
軸, 軸于C,D兩點,交直線AB于點E(位于點M右下方),連結DE交OM于點K.
軸于C,D兩點,交直線AB于點E(位于點M右下方),連結DE交OM于點K.
(1)若點M的坐標為(3,4),①求A,B兩點的坐標; ②求ME的長;
(2)若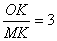 ,求∠OBA的度數;
,求∠OBA的度數;
(3)設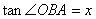 (0<
(0< <1),
<1),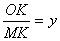 ,直接寫出
,直接寫出 關于
關于 的函數解析式.
的函數解析式.
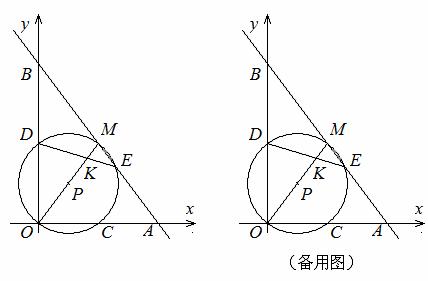
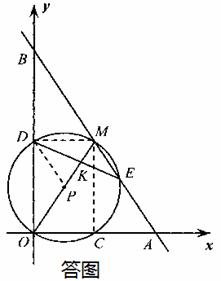 解:(1)①如答圖,連接
解:(1)①如答圖,連接 ,
,
∵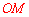 是⊙P的直徑,∴
是⊙P的直徑,∴ .
.
∵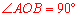 ,∴
,∴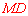 ∥
∥ ,
,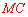 ∥
∥ .
.
∵點M是AB的中點,
∴點D是AB的中點,點C是OA的中點.
∵點M的坐標為(3,4),
∴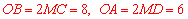 .
.
∴點B的坐標為(0,8),點A的坐標為(6,0).
②在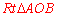 中,∵
中,∵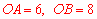 ,
,
∴由勾股定理,得 .
.
∵點M是AB的中點,∴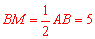 .
.
∵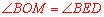 ,
, ,∴
,∴ .∴
.∴ .
.
∴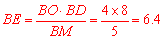 .∴
.∴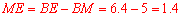 .
.
(2)如答圖,連接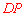 ,
,
∵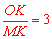 ,∴
,∴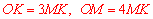 .∴
.∴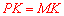 .
.
∵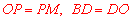 ,∴
,∴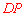 是
是 的中位線. ∴
的中位線. ∴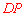 ∥
∥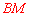 .∴
.∴
又∵ .∴
.∴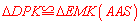 .∴
.∴ .
.
∵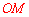 是⊙P的直徑,∴
是⊙P的直徑,∴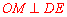 . ∴
. ∴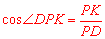 .
.
∵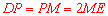 ,∴
,∴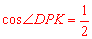 .∴
.∴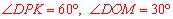 .
.
∵在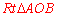 中,點M是AB的中點,∴
中,點M是AB的中點,∴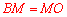 . ∴
. ∴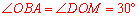 .
.
(3)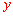 關于
關于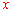 的函數解析式為
的函數解析式為 .
.
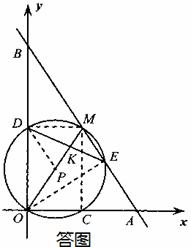
【分析】(1)①連接 ,由三角形中位線定理求得A,B兩點的坐標.
,由三角形中位線定理求得A,B兩點的坐標.
②要求ME的長,由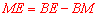 知只要求出
知只要求出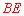 和
和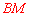 的長即可,
的長即可,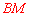 的長可由
的長可由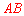 長的一半求得,而
長的一半求得,而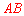 長可由勾股定理求得;
長可由勾股定理求得;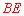 的長可由
的長可由 的對應邊成比例列式求得.
的對應邊成比例列式求得.
(2)連接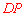 ,求得
,求得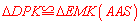 得到
得到 ,由
,由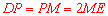 得到
得到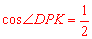 ,即
,即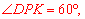 因此求得
因此求得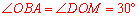 .
.
(3)如答圖,連接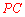 ,
,
∵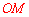 是⊙P的直徑,∴
是⊙P的直徑,∴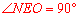 .
.
∵ (0<
(0<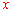 <1),不妨設
<1),不妨設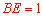 ,
,
∴在 中,
中, .
.
設 ,則
,則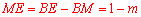 .
.
∵在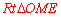 中,
中,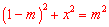 ,∴
,∴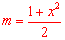 .
.
∴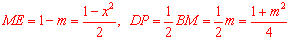 .
.
∵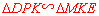 ,∴
,∴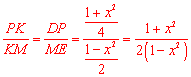 .
.
∴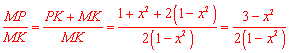 .
.
∵點P是MO的中點,∴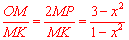 .
.
∴ .
.
∴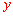 關于
關于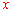 的函數解析式為
的函數解析式為 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
已知:如圖,△ABC中,AB=AC,AD是BC邊上的中線,AE∥BC,CE⊥AE;垂足為E.
(1)求證:△ABD≌△CAE;
(2)連接DE,線段DE與AB之間有怎樣的位置和數量關系?
請證明你的結論.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
某校積極開展“陽光體育”活動,共開設了跳繩、足球、籃球、跑步四種運動項目. 為了解學生最喜愛哪一種項目,隨機抽取了部分學生進行調查,并繪制了如下的條形統計圖和扇形統計圖(部分信息未給出)
(1)求本次被調查的學生人數;
(2)補全條形統計圖;
(3)該校共有1200名學生,請估計全校最喜愛籃球的人數比最喜愛足球的人數多多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,拋物線 與x軸交與A,B兩點(點A在點B的左側),與y軸交于點C. 點D和點C關于拋物線的對稱軸對稱,直線AD與y軸相交于點E.
與x軸交與A,B兩點(點A在點B的左側),與y軸交于點C. 點D和點C關于拋物線的對稱軸對稱,直線AD與y軸相交于點E.
(1)求直線AD的解析式;
(2)如圖1,直線AD上方的拋物線上有一點F,過點F作FG⊥AD于點G,作FH平行于x軸交直線AD于點H,求△FGH的周長的最大值;
(3)點M是拋物線的頂點,點P是y軸上一點,點Q是坐標平面內一點,以A,M,P,Q為頂點的四邊形是AM為邊的矩形,若點T和點Q關于AM所在直線對稱,求點T的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com