
【題目】如圖,拋物線![]() 經過點兩點
經過點兩點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是拋物線上一個動點,設點
是拋物線上一個動點,設點![]() 的橫坐標為
的橫坐標為![]() .連接
.連接![]()
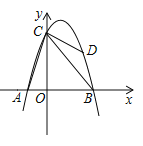
(1)求拋物線的函數表達式;
(2)當![]() 的面積等于
的面積等于![]() 的面積時,求
的面積時,求![]() 的值;
的值;
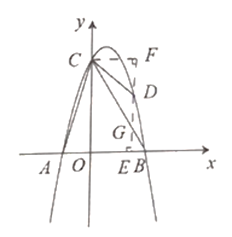
(3)當![]() 時,若點
時,若點![]() 是
是![]() 軸正半軸上上的一個動點,點
軸正半軸上上的一個動點,點![]() 是拋物線上動點,試判斷是否存在這樣的點
是拋物線上動點,試判斷是否存在這樣的點![]() ,使得以點
,使得以點![]() 為頂點的四邊形是平行四邊形.若存在,請直接寫出點
為頂點的四邊形是平行四邊形.若存在,請直接寫出點![]() 的坐標:若不存在,請說明理由.
的坐標:若不存在,請說明理由.
【答案】(1)![]() ;(2)2;(3)存在,點
;(2)2;(3)存在,點![]() 的坐標為
的坐標為![]()
【解析】
(1)由拋物線交點式表達,即可求解;
(2)利用![]() ,即可求解;
,即可求解;
(3)分BD是平行四邊形的一條邊、BD是平行四邊形的對角線兩種情況,分別求解即可.
(1)拋物線![]() 經過點
經過點![]()
![]()
解得: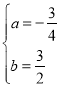
![]() 拋物線的函數表達式為
拋物線的函數表達式為![]()
(2)作直線![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,作
,作![]() ,垂足為
,垂足為![]() ,
,
![]() 點
點![]() 的坐標為為
的坐標為為![]()
![]()
由![]() 得.
得.![]()
![]() 點
點![]() 的坐標為
的坐標為![]()
![]()
![]()
![]()
![]()
設直線![]() 的函數表達式為
的函數表達式為![]()
由![]() 兩點的坐標得
兩點的坐標得![]()
解得: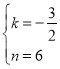
![]() 直線
直線![]() 的函數表達式為
的函數表達式為![]()
![]() 點
點![]() 的坐標為
的坐標為![]()
![]()
![]() 點
點![]() 的坐標為
的坐標為![]()
![]()
![]()
![]()
![]()
![]() 解得
解得![]()
![]() 的值為
的值為![]() .
.
(3)存在,(方法多種,以下從對角線出發來求解)
以![]() 以為平行四邊形的對角線時,設點
以為平行四邊形的對角線時,設點![]() 分別是
分別是![]() 、
、![]() 和的中點,
和的中點,
則:![]() ,
,
![]()
易求得: ![]() 或
或![]() (舍去);
(舍去);
以![]() 為平行四邊形的對角線時,同理求得:
為平行四邊形的對角線時,同理求得: ![]() 或4 (均舍去);
或4 (均舍去);
以![]() 為平行四邊形的對角線時,同理求得:
為平行四邊形的對角線時,同理求得: ![]() 或
或![]() (舍去)
(舍去)
綜上,點![]() 的坐標為
的坐標為![]()


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a,b,c是常數,a≠0)圖象的一部分,與x軸的交點A在點(2,0)和(3,0)之間,對稱軸是x=1.對于下列說法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m為實數);⑤當﹣1<x<3時,y>0,其中正確的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,點O為坐標原點,直線y=﹣x+3交x軸于點B,交y軸于點A,過點A作AC⊥AB交x軸于點C.
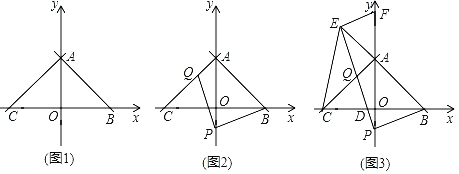
(1)如圖1,求直線AC的解析式;
(2)如圖2,點P在AO的延長線上,點Q在AC上,連接PB,PQ,且PQ=PB,設點P的縱坐標為t,AQ的長為d,求d與t之間的函數關系式(不要求寫出自變量t的取值范圍);
(3)如圖3,在(2)的條件下,PQ交x軸于點D,延長PQ交BA的延長線于點E,過點E作EF⊥PE交y軸于點F,若DE=![]() EF,求點Q的坐標.
EF,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
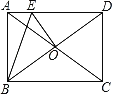
【題目】如圖,矩形ABCD的對角線AC與BD交于點O,點E在AD上,且DE=CD,連接OE,∠ABE=![]() ∠ACB,若AE=2,則OE的長為_____.
∠ACB,若AE=2,則OE的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】央視熱播節目“朗讀者”激發了學生的閱讀興趣,某校為滿足學生的閱讀需求,欲購進一批學生喜歡的圖書,學校組織學生會成員隨機抽取部分學生進行問卷調查,被調查學生須從“文史類、社科類、小說類、生活類”中選擇自己喜歡的一類,根據調查結果繪制了統計圖(未完成),請根據圖中信息,解答下列問題
(1)此次共調查了 名學生;
(2)將條形統計圖1補充完整;
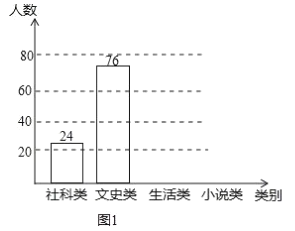
(3)圖2中“社科類”所在扇形的圓心角為 度;
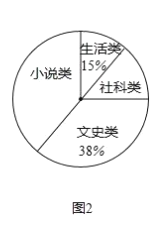
(4)若該校共有學生![]() 人,估計該校喜歡“社科類”書籍的學生人數.
人,估計該校喜歡“社科類”書籍的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
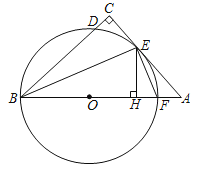
【題目】如圖,在△ABC中,∠C=90°,∠ABC的平分線交AC于點E,過點E作BE的垂線交AB于點F,⊙O是△BEF的外接圓.
(1)求證:AC是⊙O的切線;
(2)過點E作EH⊥AB,垂足為H,若CD=1,EH=3,求BE長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個三角形一條邊的平方等于另兩條邊的乘積,我們把這個三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,請直接寫出所有滿足條件的AC的長;
,請直接寫出所有滿足條件的AC的長;
![]() 如圖1,在四邊形ABCD中,
如圖1,在四邊形ABCD中,![]() ,對角線BD平分
,對角線BD平分![]() ,
,![]() 求證:
求證:![]() 是比例三角形.
是比例三角形.
![]() 如圖2,在
如圖2,在![]() 的條件下,當
的條件下,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=3,BC=2,沿對角線AC剪開(如圖①);固定△ADC,把△ABC沿AD方向平移(如圖②),當兩個三角形重疊部分的面積最大時,移動的距離AA′等于( )

A. 1 B. 1.5 C. 2 D. 0.8或1.2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com