
【題目】如圖,在△ABC中,∠C=90°,AD是∠BAC的平分線,O是AB上一點,以OA為半徑的⊙O經過點D。
(1)求證:BC是⊙O切線;
(2)若BD=5, DC=3,求AC的長。
【答案】
(1)證明: 如圖1,連接OD.
∵ OA=OD, AD平分∠BAC,
∴ ∠ODA=∠OAD, ∠OAD=∠CAD,
∴ ∠ODA=∠CAD,
∴ OD//AC,
∴ ∠ODB=∠C=90°,
∴ BC是⊙O的切線;
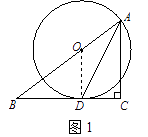
(2)解:如圖2,過D作DE⊥AB于E.
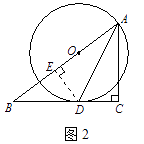
∴ ∠AED=∠C=90°,
又∵ AD=AD, ∠EAD=∠CAD,
∴ △AED≌△ACD.
∴ AE=AC, DE=DC=3,在Rt△BED中,∠BED =90°,由勾股定理,得BE= ![]() .設AC=x(x>0), 則AE=x,在Rt△ABC中,∠C=90°, BC=BD+DC=8, AB=x+4, 由勾股定理,得
.設AC=x(x>0), 則AE=x,在Rt△ABC中,∠C=90°, BC=BD+DC=8, AB=x+4, 由勾股定理,得 ![]() ,
,
解得x=6,即 AC=6.
【解析】(1)要證BC是⊙O切線,點D在圓上,因此連接OD,需證明OD⊥BC。先根據等腰三角形的性質及角平分線的定義,證明∠ODA=∠CAD,再根據平行線的判定及性質證明∠ODB=∠C=90°,即可得出結論。
(2)抓住已知AD是∠BAC的平分線,DC⊥AC,根據角平分線的性質添加輔助線過D作DE⊥AB于E,得出DE=DC=3,根據勾股定理求出BE的長,再證明△AED≌△ACD,得出AE=AC,然后在Rt△ABC中,根據勾股定理即可求出AC的長。
【考點精析】通過靈活運用平行線的判定與性質和角平分線的性質定理,掌握由角的相等或互補(數量關系)的條件,得到兩條直線平行(位置關系)這是平行線的判定;由平行線(位置關系)得到有關角相等或互補(數量關系)的結論是平行線的性質;定理1:在角的平分線上的點到這個角的兩邊的距離相等; 定理2:一個角的兩邊的距離相等的點,在這個角的平分線上即可以解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某居民小區為了綠化小區環境,建設和諧家園,準備將一塊周長為76米的長方形空地,設計成長和寬分別相等的9塊小長方形,如圖所示,計劃在空地上種上各種花卉,經市場預測,綠化每平方米空地造價210元,請計算,要完成這塊綠化工程,預計花費多少元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,若![]() ,將點
,將點![]() 在
在![]() 內部,∠
內部,∠![]() ,∠
,∠![]() ,∠
,∠![]() 滿足的數量關系是 ,并說明理由.
滿足的數量關系是 ,并說明理由.
(2)在如圖1中,將直線![]() 繞點
繞點![]() 逆時針方向旋轉一定角度交直線
逆時針方向旋轉一定角度交直線![]() 于點
于點![]() ,如圖2,利用(1)中的結論(可以直接套用),求∠
,如圖2,利用(1)中的結論(可以直接套用),求∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() 之間有何數量關系?
之間有何數量關系?

(3)科技活動課上,雨軒同學制作了一個圖(3)的“飛旋鏢”,經測量發現∠![]() =
=![]() °,∠
°,∠![]() =
=![]() °,則∠
°,則∠![]() 與∠
與∠![]() 的數量關系是 .
的數量關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形組成的網格中,△AOB的頂點均在格點上,點A、B的坐標分別是A (3,2)、B(1,3)。△AOB繞點O 逆時針旋轉90°后得到△A1OB1.
(1)畫出旋轉后的圖形;
(2)求線段OB在旋轉過程中所掃過的圖形面積(寫過程)。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩家快遞公司攬件員(攬收快件的員工)的日工資方案如下:
甲公司為“基本工資+攬件提成”,其中基本工資為70元/日,每攬收一件提成2元;
乙公司無基本工資,僅以攬件提成計算工資.若當日攬件數不超過40,每件提成4元;若當日攪件數超過40,超過部分每件多提成2元.
如圖是今年四月份甲公司攬件員人均攬件數和乙公司攪件員人均攬件數的條形統計圖:
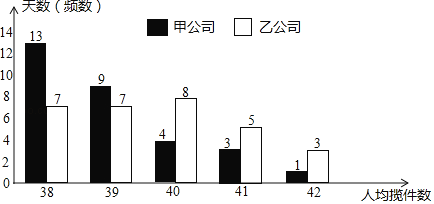
(1)現從今年四月份的30天中隨機抽取1天,求這一天甲公司攬件員人均攬件數超過40(不含40)的概率;
(2)根據以上信息,以今年四月份的數據為依據,并將各公司攬件員的人均攬件數視為該公司各攬件員的
攬件數,解決以下問題:
①估計甲公司各攬件員的日平均件數;
②小明擬到甲、乙兩家公司中的一家應聘攬件員,如果僅從工資收入的角度考慮,請利用所學的統計知識幫他選擇,井說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B在反比例函數 ![]() 的圖象上,且點A、B的橫坐標分別為a、2a(a>0),AC⊥x軸,垂足為C,且△AOC的面積為2,
的圖象上,且點A、B的橫坐標分別為a、2a(a>0),AC⊥x軸,垂足為C,且△AOC的面積為2,
(1)求該反比例函數的解析式;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線MN與直線AB、CD分別交于點E、F,∠1與∠2互補.
(1)試判斷直線AB與直線CD的位置關系,并說明理由;
(2)如圖2,∠BEF與∠EFD的角平分線交于點P,EP與CD交于點G,點H是MN上一點,且GH⊥EG,求證:PF∥GH;
(3)如圖3,在(2)的條件下,連接PH,K是GH上一點使∠PHK=∠HPK,作PQ平分∠EPK,問∠HPQ的大小是否發生變化?若不變,請求出其值;若變化,說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com