
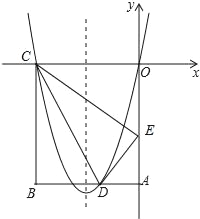
【題目】如圖,在矩形OABC中,OA=5,AB=4,點D為邊AB上一點,將△BCD沿直線CD折疊,使點B恰好落在OA邊上的點E處,分別以OC,OA所在的直線為x軸,y軸建立平面直角坐標系.
(1)求點E坐標及經過O,D,C三點的拋物線的解析式;
(2)一動點P從點C出發,沿CB以每秒2個單位長的速度向點B運動,同時動點Q從E點出發,沿EC以每秒1個單位長的速度向點C運動,當點P到達點B時,兩點同時停止運動.設運動時間為t秒,當t為何值時,DP=DQ;
(3)若點N在(2)中的拋物線的對稱軸上,點M在拋物線上,是否存在這樣的點M與點N,使得以M,N,C,E為頂點的四邊形是平行四邊形?若存在,請求出M點的坐標;若不存在,請說明理由.
【答案】(1)E(0,﹣3),拋物線解析式為y=![]() x2+
x2+![]() x;(2)
x;(2)![]() ;(3)存在滿足條件的點M,其坐標為(2,16)或(﹣6,16)或(﹣2,﹣
;(3)存在滿足條件的點M,其坐標為(2,16)或(﹣6,16)或(﹣2,﹣![]() ).
).
【解析】
(1)由折疊的性質可得CE,CO的長,在Rt△COE中,由勾股定理可求得OE,即點E的坐標,設AD=m,在Rt△ADE中,由勾股定理可得m的值,即可得點D的坐標,結合C,O兩點,利用待定系數法即可求得拋物線的解析式;
(2)用t表示出CP,BP的長,可證明Rt△DBP≌Rt△DEQ,得到BP=EQ,即可求的t的值;
(3)可設出N點的坐標,分三種情況①EN為對角線,②EM為對角線,③EC為對角線,根據平行四邊形的性質可求得對角線的交點橫坐標,從而可求得M點的橫坐標,再代入拋物線解析式即可求得點M的坐標.
(1)∵CE=CB=5,CO=AB=4,
∴在Rt△COE中,
OE=![]() =3,
=3,
∴E(0,﹣3),
設AD=m,則DE=BD=4﹣m,
∵OE=3,
∴AE=5﹣3=2,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,
即m2+22=(4﹣m)2,解得m=![]() ,
,
∴D(﹣![]() ,﹣5),
,﹣5),
∵C(﹣4,0),O(0,0),
∴設過O、D、C三點的拋物線為y=ax(x+4),
∴﹣5=﹣![]() a(﹣
a(﹣![]() +4),解得a=
+4),解得a=![]() ,
,
∴拋物線解析式為y=![]() x(x+4)=
x(x+4)=![]() x2+
x2+![]() x;
x;
(2)∵CP=2t,
∴BP=5﹣2t,
∵BD=![]() ,DE=
,DE=![]() =
=![]() ,
,
∴BD=DE,
在Rt△DBP和Rt△DEQ中,![]() ,
,
∴Rt△DBP≌Rt△DEQ(HL),
∴BP=EQ,
∴5﹣2t=t,
∴t=![]() ;
;
(3)∵拋物線的對稱為直線x=﹣2,
∴設N(﹣2,n),
又由題意可知C(﹣4,0),E(0,﹣3),設M(m,y),
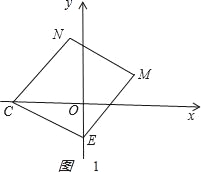
①當EN為對角線,即四邊形ECNM是平行四邊形時,如圖1,
 ,
,
則線段EN的中點
橫坐標為![]() =﹣1,線段CM中點橫坐標為
=﹣1,線段CM中點橫坐標為![]() ,
,
∵EN,CM互相平分,
∴![]() =﹣1,解得m=2,
=﹣1,解得m=2,
又M點在拋物線上,
∴y=![]() ×22+
×22+![]() ×2=16,
×2=16,
∴M(2,16);
②當EM為對角線,即四邊形ECMN是平行四邊形時,如圖2,
 ,
,
則線段EM的中點,
橫坐標為![]() =
=![]() m,線段CN中點橫坐標為
m,線段CN中點橫坐標為![]() =﹣3,
=﹣3,
∵EN,CM互相平分,
∴![]() m=﹣3,解得m=﹣6,
m=﹣3,解得m=﹣6,
又∵M點在拋物線上,
∴y=![]() ×(﹣6)2+
×(﹣6)2+![]() ×(﹣6)=16,
×(﹣6)=16,
∴M(﹣6,16);
③當CE為對角線,即四邊形EMCN是平行四邊形時,
則M為拋物線的頂點,即M(﹣2,﹣![]() ).
).
綜上可知,存在滿足條件的點M,其坐標為(2,16)或(﹣6,16)或(﹣2,﹣![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖,已知點A(0,2),B(2,2),C(-1,-2),拋物線F:y=x2-2mx+m2-2與直線x=-2交于點P.
(1)當拋物線F經過點C時,求它的解析式;
(2)設點P的縱坐標為yP,求yP的最小值,此時拋物線F上有兩點(x1,y1),(x2,y2),且x1<x2≤-2,比較y1與y2的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年的6月5日為世界環保日,為了提倡低碳環保,某公司決定購買10臺節省能源的新設備,現有甲、乙兩種型號的設備可供選購. 經調查:購買3臺甲型設備比購買2臺乙型設備多花16萬元,購買2臺甲型設備比購買3臺乙型設備少花6萬元.
(1)求甲、乙兩種型號設備的價格;
(2)該公司經預算決定購買節省能源的新設備的資金不超過110萬元,你認為該公司有哪幾種購買方案;
(3)在(2)的條件下,已知甲型設備的產量為240噸/月,乙型設備的產量為180噸/月.若每月要求總產量不低于2040噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區對即將參加中考的5000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和不完整的頻數分布直方圖,請根據圖表信息回答下列問題:
初中畢業生視力抽樣調查頻數分布表
視力 | 頻數(人) | 頻率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次調查的樣本容量為 ;
(2)在頻數分布表中,a= ,b= ,并將頻數分布直方圖補充完整;
(3)若視力在4.6以上(含4.6)均屬正常,根據上述信息估計全區初中畢業生中視力正常的學生有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若等腰三角形的頂角為36°,則這個三角形就是黃金三角形。如圖,在△ABC中,BA=BC,D 在邊 CB 上,且 DB=DA=AC。

(1)如圖1,寫出圖中所有的黃金三角形,并證明;
(2)若 M為線段 BC上的點,過 M作直線MH⊥AD于 H,分別交直線 AB,AC與點N,E,如圖 2,試寫出線段 BN、CE、CD之間的數量關系,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=2,∠B=∠C=40°,點D在線段BC上運動(D不與B、C重合),連接AD,作∠ADE=40°,DE交線段AC于E.
(1)當∠BDA=115°時,∠EDC=______°,∠DEC=______°;點D從B向C運動時,∠BDA逐漸變______(填“大”或“小”);
(2)當DC等于多少時,△ABD≌△DCE,請說明理由;
(3)在點D的運動過程中,△ADE的形狀可以是等腰三角形嗎?若可以,請直接寫出∠BDA的度數.若不可以,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
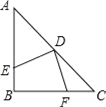
【題目】如圖,在等腰三角形ABC中,∠ABC=90°,D為AC邊上中點,過D點作DE⊥DF,交AB于E,交BC于F,若S四邊形BFDE=9,則AB的長為:
A. 3 B. 6 C. 9 D. 18
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,AC為對角線,延長CD至點E使CE=CA,連接AE。F為AB上一點,且BF=DE,連接FC.
(1)若DE=1,CF=2![]() ,求CD的長。
,求CD的長。
(2)如圖2,點G為線段AE的中點,連接BG交AC于H,若∠BHC+∠ABG=600,求證:AF+CE=![]() AC.
AC.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據對徐州市相關的市場物價調研,預計進入夏季后的某一段時間,某批發市場內的甲種蔬菜的銷售利潤y1(千元)與進貨量x(噸)之間的函數![]() 的圖象如圖①所示,乙種蔬菜的銷售利潤y2(千元)與進貨量x(噸)之間的函數
的圖象如圖①所示,乙種蔬菜的銷售利潤y2(千元)與進貨量x(噸)之間的函數![]() 的圖象如圖②所示.
的圖象如圖②所示.

(1)分別求出y1、y2與x之間的函數關系式;
(2)如果該市場準備進甲、乙兩種蔬菜共10噸,設乙種蔬菜的進貨量為t噸,寫出這兩種蔬菜所獲得的銷售利潤之和W(千元)與t(噸)之間的函數關系式,并求出這兩種蔬菜各進多少噸時 獲得的銷售利潤之和最大,最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com