
【題目】已知在△ABC中,∠A,∠B,∠C的對邊分別是a,b,c,關于x的方程a(1﹣x2)+2bx+c(1+x2)=0有兩個相等實根,且3c=a+3b
(1)試判斷△ABC的形狀;
(2)求sinA+sinB的值.
【答案】(1)△ABC為直角三角形;(2)![]() .
.
【解析】
(1)先把方程整理為一般式,再根據判別式的意義得到△=![]() ,則
,則![]() ,然后根據勾股定理的逆定理判斷三角形形狀;
,然后根據勾股定理的逆定理判斷三角形形狀;
(2)由于![]() ,3c=a+3b,消去a得
,3c=a+3b,消去a得![]() ,變形為(4c5b)(cb)=0,則b=
,變形為(4c5b)(cb)=0,則b=![]() ,a=
,a=![]() ,根據正弦的定義得sinA=
,根據正弦的定義得sinA=![]() ,sinB=
,sinB=![]() ,所以sinA+sinB=
,所以sinA+sinB=![]() ,然后把b=
,然后把b=![]() ,a=
,a=![]() 代入計算即可.
代入計算即可.
解:(1)方程整理為(c﹣a)x2+2bx+a+c=0,
根據題意得△=4b2﹣4(c﹣a)(a+c)=0,
∴a2+b2=c2,
∴△ABC為直角三角形;
(2)∵a2+b2=c2,3c=a+3b
∴(3c﹣3b)2+b2=c2,
∴(4c﹣5b)(c﹣b)=0,
∴4c=5b,即b=![]() c,
c,
∴a=3c﹣3b=![]() c
c
∵sinA=![]() ,sinB=
,sinB=![]() ,
,
∴sinA+sinB=![]() .
.


科目:初中數學 來源: 題型:
【題目】在直角坐標系xOy中,已知點P是反比例函數y=![]() (x>0)圖象上一個動點,以P為圓心的圓始終與y軸相切,設切點為A.
(x>0)圖象上一個動點,以P為圓心的圓始終與y軸相切,設切點為A.
(1)如圖1,當⊙P運動到與x軸相切,設切點為K,試判斷四邊形OKPA的形狀,并說明理由;
(2)如圖2,當⊙P運動到與x軸相交,設交點為點B、C.當四邊形ABCP是菱形時,求出點A、B、C的坐標;
(3)在(2)的條件下,求出經過A、B、C三點的拋物線的解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數的圖象如圖所示,對稱軸為x=1,給出下列結論:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0..其中正確的結論有:
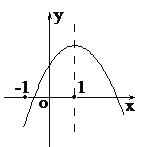
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程![]() .
.
(1)請你為m選取一個合適的整數,使得到的方程有兩個不相等的實數根;
(2)設![]() 、
、![]() 是
是![]() 中你所得到的方程的兩個實數根,求:
中你所得到的方程的兩個實數根,求:![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
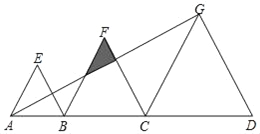
【題目】如圖,點B、C是線段AD上的點,△ABE、△BCF、△CDG都是等邊三角形,且AB=4,BC=6,已知△ABE與△CDG的相似比為2:5.則
①CD=____;
②圖中陰影部分面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年以來,我國持續大面積的霧霾天氣讓環保和健康問題成為焦點.為了調查學生對霧霾天氣知識的了解程度,某校在學生中做了一次抽樣調查,調查結果共分為四個等級:A.非常了解;B.比較了解;C.基本了解;D.不了解.根據調查統計結果,繪制了不完整的三種統計圖表.
對霧霾了解程度的統計表:
對霧霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比較了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
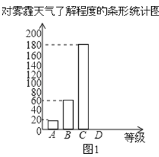
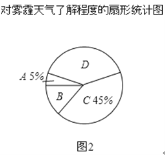
請結合統計圖表,回答下列問題.
(1)本次參與調查的學生共有 人,m= ,n= ;
(2)圖2所示的扇形統計圖中D部分扇形所對應的圓心角是 度;
(3)請補全條形統計圖;
(4)根據調查結果,學校準備開展關于霧霾知識競賽,某班要從“非常了解”態度的小明和小剛中選一人參加,現設計了如下游戲來確定,具體規則是:把四個完全相同的乒乓球標上數字1,2,3,4,然后放到一個不透明的袋中,一個人先從袋中隨機摸出一個球,另一人再從剩下的三個球中隨機摸出一個球.若摸出的兩個球上的數字和為奇數,則小明去;否則小剛去.請用樹狀圖或列表法說明這個游戲規則是否公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
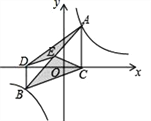
【題目】如圖,點A,B在反比例函數![]() (k>0)的圖象上,AC⊥x軸,BD⊥x軸,垂足C,D分別在x軸的正、負半軸上,CD=k,已知AB=2AC,E是AB的中點,且△BCE的面積是△ADE的面積的2倍,則k的值是______.
(k>0)的圖象上,AC⊥x軸,BD⊥x軸,垂足C,D分別在x軸的正、負半軸上,CD=k,已知AB=2AC,E是AB的中點,且△BCE的面積是△ADE的面積的2倍,則k的值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明從家步行到校車站臺,等候坐校車去學校,圖中的折線表示這一過程中小明的路程S(km)與所花時間t(min)間的函數關系;下列說法:①他步行了1km到校車站臺;②他步行的速度是100m/min;③他在校車站臺等了6min;④校車運行的速度是200m/min;其中正確的個數是( )個.
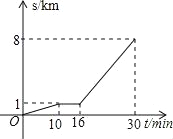
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據揚州市某風景區的旅游信息,![]() 公司組織一批員工到該風景區旅游,支付給旅行社
公司組織一批員工到該風景區旅游,支付給旅行社![]() 元.
元. ![]() 公司參加這次旅游的員工有多少人?
公司參加這次旅游的員工有多少人?
揚州市某風景區旅游信息表
旅游人數 | 收費標準 |
不超過 | 人均收費 |
超過 | 每增加 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com