


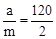 ,即
,即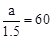 ,解得a=90。
,解得a=90。 ,解得n=3.5。
,解得n=3.5。 ,解得
,解得 。
。 ,解得
,解得 。
。 。
。

 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案科目:初中數學 來源:不詳 題型:解答題
 ,第8天時,雨雪停止附近的勝利農場前來支援,合作6天,完成了興化農場所有的收割任務.圖1是機械收割的畝數y1(畝)和人工收割的畝數y2(畝)與時間x(天)之間的函數圖象.圖2是剩余的農作物的畝數w(畝)與時間x天之間的函數圖象,請結合圖象回答下列問題.
,第8天時,雨雪停止附近的勝利農場前來支援,合作6天,完成了興化農場所有的收割任務.圖1是機械收割的畝數y1(畝)和人工收割的畝數y2(畝)與時間x(天)之間的函數圖象.圖2是剩余的農作物的畝數w(畝)與時間x天之間的函數圖象,請結合圖象回答下列問題.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 經過點D(6,1),點C是雙曲線第三象限分支上的動點,過C作CA⊥x軸,過D作DB⊥y軸,垂足分別為A,B,連接AB,BC.
經過點D(6,1),點C是雙曲線第三象限分支上的動點,過C作CA⊥x軸,過D作DB⊥y軸,垂足分別為A,B,連接AB,BC.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
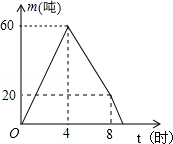
| A.8.4小時 | B.8.6小時 | C.8.8小時 | D.9小時 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com