
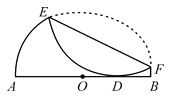
【題目】如圖,已知半圓O的直徑AB=4,沿它的一條弦折疊.若折疊后的圓弧與直徑AB相切于點D,且AD:DB=3:1,則折痕EF的長______.
【答案】![]() .
.
【解析】
解:如圖,過O作弦BC的垂線OP,垂足為D,分別與弧的交點為A、G,過切點F作PF⊥半徑OC交OP于P點,
∵OP⊥BC,∴BD=DC,即OP為BC的中垂線. ∴OP必過弧BGC所在圓的圓心
又∵OE為弧BGC所在圓的切線,PF⊥OE,∴PF必過弧BGC所在圓的圓心
∴點P為弧BGC所在圓的圓心
∵弧BAC沿BC折疊得到弧BGC,∴⊙P為半徑等于⊙O的半徑,即PF=PG=OE=2,并且AD=GD
∴OG=AP
而F點分⊙O的直徑為3:1兩部分,∴OF=1
在Rt△OPF中,設(shè)OG=x,則OP=x+2,
∴OP2=OF2+PF2,即(x+2)2=12+22,解得x=![]()
∴AG=2-(![]() )=
)=![]()
∴DG=![]()
∴OD=OG+DG=![]()
在Rt△OBD中,BD2=OB2+OD2,即BD2=22-(![]() )2,
)2,
∴BD=![]()
∴BC=2BD=![]()
故答案為:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知銳角∠AOB如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;
,交射線OB于點D,連接CD;
(2)分別以點C,D為圓心,CD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接OM,MN.
根據(jù)以上作圖過程及所作圖形,下列結(jié)論中錯誤的是( )

A. ∠COM=∠CODB. 若OM=MN,則∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】發(fā)現(xiàn) 對于2,4,6三個連續(xù)的偶數(shù)來說,可以得到![]() ;即前兩個偶數(shù)的和等于第三個偶數(shù);對于8,10,12,14,16五個連續(xù)的偶數(shù)來說,可以得到
;即前兩個偶數(shù)的和等于第三個偶數(shù);對于8,10,12,14,16五個連續(xù)的偶數(shù)來說,可以得到![]() ,即前三個偶數(shù)的和等于后兩個偶數(shù)的和.…
,即前三個偶數(shù)的和等于后兩個偶數(shù)的和.…
驗證 對于九個連續(xù)偶數(shù)來說,若前五個偶數(shù)的和等于后四個偶數(shù)的和,則中間的偶數(shù)是_______;
延伸 是否存在連續(xù)的五個奇數(shù),使得前三個奇數(shù)的和等于后兩個奇數(shù)的和.若有,寫出這五個奇數(shù);若沒有,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線![]() 相交于
相交于![]() ,在直線
,在直線![]() 上分別取點
上分別取點![]() ,使
,使![]() ,分別過點A,B作直線
,分別過點A,B作直線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() ,設(shè)
,設(shè)![]() .
.
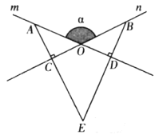
(1)求證:![]() ;
;
(2)小明說,不論![]() 是銳角還是鈍角,點
是銳角還是鈍角,點![]() 都在
都在![]() 的平分線上,你認(rèn)為他說的有道理嗎?并說明理由.
的平分線上,你認(rèn)為他說的有道理嗎?并說明理由.
(3)連接![]() ,當(dāng)
,當(dāng)![]() 與三角板的形狀相同時,直接寫出
與三角板的形狀相同時,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 與x軸交于點
與x軸交于點![]() ,點
,點![]() ,與y軸交于點C,且過點
,與y軸交于點C,且過點![]() .點P、Q是拋物線
.點P、Q是拋物線![]() 上的動點.
上的動點.
(1)求拋物線的解析式;
(2)當(dāng)點P在直線OD下方時,求![]() 面積的最大值.
面積的最大值.
(3)直線OQ與線段BC相交于點E,當(dāng)![]() 與
與![]() 相似時,求點Q的坐標(biāo).
相似時,求點Q的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某城市為了解游客人數(shù)的變化規(guī)律,提高旅游服務(wù)質(zhì)量,收集并整理了2014年1月至2016年12月期間月接待游客量(單位:萬人)的數(shù)據(jù),繪制了下面的折線圖:
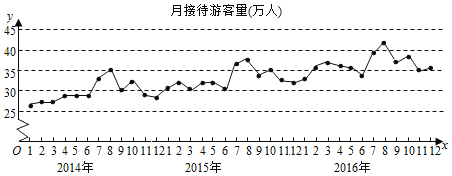
根據(jù)該折線圖,下列結(jié)論錯誤的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月份
D.各年1月至6月的月接待游客量相對7月至12月,波動性更小,變化比較平穩(wěn)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某水果公司新購進10000千克柑橘,每千克柑橘的成本為9元. 柑橘在運輸、存儲過程中會有損壞,銷售人員從所有的柑橘中隨機抽取若干柑橘,進行“柑橘損壞率”統(tǒng)計,并把獲得的數(shù)據(jù)記錄如下:
柑橘總重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
損壞柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘損壞的頻率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根據(jù)以上數(shù)據(jù),估計柑橘損壞的概率為 (結(jié)果保留小數(shù)點后一位);由此可知,去掉損壞的柑橘后,水果公司為了不虧本,完好柑橘每千克的售價至少為________元.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖, 在三邊互不相等的△ABC中, D,E,F分別是AB,AC,BC邊的中點.連接DE,過點C作CM∥AB交DE的延長線于點M,連接CD、EF交于點N,則圖中全等三角形共有( )
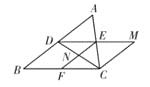
A.3對B.4對C.5對D.6對
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com