
【題目】已知:如圖,在平面直角坐標系xOy中,反比例函數![]() 的圖象與一次函數y2=kx+b的圖象交于點A(-4,-1)和點B(1,n).
的圖象與一次函數y2=kx+b的圖象交于點A(-4,-1)和點B(1,n).
(1)求這兩個函數的表達式;
(2)觀察圖象,當y1>y2時,直接寫出自變量x的取值范圍;
(3)如果點C與點A關于y軸對稱,求△ABC的面積.

【答案】(1)y1=![]() ,y2=x+3;(2)x<﹣4 或0<x <1;(3)20
,y2=x+3;(2)x<﹣4 或0<x <1;(3)20
【解析】試題分析:(1)把A的坐標代入![]() 中即可求出m的值,即可得到y1的函數解析式,再把B的橫坐標代入y1中即可求出n的值,再將A、B兩點坐標代入y2中即可求出k、b的值;(2)寫出圖像中y1的圖像在y2圖像上面時x的取值范圍即可;(3)作BD⊥AC于點D,S△ABC=
中即可求出m的值,即可得到y1的函數解析式,再把B的橫坐標代入y1中即可求出n的值,再將A、B兩點坐標代入y2中即可求出k、b的值;(2)寫出圖像中y1的圖像在y2圖像上面時x的取值范圍即可;(3)作BD⊥AC于點D,S△ABC=![]() AC·BD=
AC·BD=![]() ×8×5=20即可;
×8×5=20即可;
試題解析:
解:(1)∵函數![]() 的圖象過點A(-4,-1),
的圖象過點A(-4,-1),
∴m=4, ∴y1=![]() ,
,
又∵點B(1,n)在y1=![]() 上,
上,
∴n=4, ∴B(1,4)
又∵一次函數y2=kx+b過A,B兩點,
即, ![]() 解之得
解之得![]() .
.
∴y2=x+3.
綜上可得y1=![]() ,y2=x+3.
,y2=x+3.
(2)要使y1>y2,即函數y1的圖象總在函數y2的圖象上方,
∴x<﹣4 或0 < x <1.
(3)作BD⊥AC于點D,如圖所示:

∵AC=8,BD=5,
∴△ABC的面積S△ABC=![]() AC·BD=
AC·BD=![]() ×8×5=20.
×8×5=20.


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
【題目】某班“數學興趣小組”對函數y=x2﹣2|x|的圖象和性質進行了探究,探究過程如下,請補充完整.(1)自變量x的取值范圍是全體實數,x與y的幾組對應值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根據表中數據,在如圖所示的平面直角坐標系中描點,并畫出了函數圖象的一部分,請畫出該函數圖象的另一部分.
(3)觀察函數圖象,寫出兩條函數的性質.
(4)進一步探究函數圖象發現:
①函數圖象與x軸有 個交點,所以對應的方程x2﹣2|x|=0有 個實數根;
②方程x2﹣2|x|=2有 個實數根.

③關于x的方程x2﹣2|x|=a有4個實數根時,a的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A,B,C三名大學生競選系學生會主席,他們的筆試成績和口試成績(單位:分)分別用了兩種方式進行了統計,如表和圖一:
A | B | C | |
筆試 | 85 | 95 | 90 |
口試 | 80 | 85 |

(1)請將表一和圖一中的空缺部分補充完整.
(2)競選的最后一個程序是由本系的300名學生進行投票,三位候選人的得票情況如圖二(沒有棄權票,每名學生只能推薦一個),請計算每人的得票數.
(3)若每票計1分,系里將筆試、口試、得票三項測試得分按4:3:3的比例確定個人成績,請計算三位候選人的最后成績,并根據成績判斷誰能當選.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在5×5的正方形網格中,每個小正方形的邊長都是1,在所給網格中按下列要求畫出圖形: 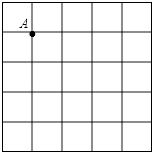
(1)(I)已知點A在格點(即小正方形的頂點)上,畫一條線段AB,長度為 ![]() ,且點B在格點上; (II)以上題中所畫線段AB為一邊,另外兩條邊長分別是3,2
,且點B在格點上; (II)以上題中所畫線段AB為一邊,另外兩條邊長分別是3,2 ![]() ,畫一個三角形ABC,使點C在格點上(只需畫出符合條件的一個三角形);
,畫一個三角形ABC,使點C在格點上(只需畫出符合條件的一個三角形);
(2)所畫的三角形ABC的AB邊上高線長為(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),在矩形ABCD中,AB=4,BC=6,P是AD的中點,N是BC延長線上一點,連結PN,過點P作PN的垂線,交AB于點E,交CD的延長線于點F,連結EN,FN,設CN=x,AE=y.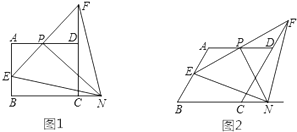
(1)求證:PE=PF;
(2)當0<x< ![]() 時,求y關于x的函數表達式;
時,求y關于x的函數表達式;
(3)若將“矩形ABCD”變為“菱形ABCD”,如圖(2),AB=BC=4,∠B=60°,當0<x<3時,其它條件不變,求此時y關于x的函數表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com