
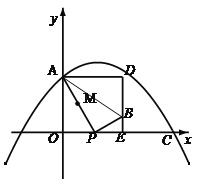
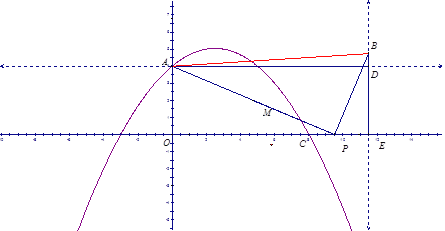
【題目】如圖,在平面直角坐標系xOy中,拋物線y=ax2+![]() x+c過點A(0,4)和C(8,0),P(t,0)是x軸正半軸上的一個動點,M是線段AP的中點,將線段MP繞點P順時針旋轉90°得線段PB.過點B作x軸的垂線、過點A作y軸的垂線,兩直線相交于點D.
x+c過點A(0,4)和C(8,0),P(t,0)是x軸正半軸上的一個動點,M是線段AP的中點,將線段MP繞點P順時針旋轉90°得線段PB.過點B作x軸的垂線、過點A作y軸的垂線,兩直線相交于點D.
(1)求此拋物線的對稱軸;
(2)當t為何值時,點D落在拋物線上?
(3)是否存在t,使得以A、B、D為頂點的三角形與△PEB相似?若存在,求此時t的值;若不存在,請說明理由.

【答案】(1)對稱軸為:x=![]() ;(2)當t=3時,點D落在拋物線上;(3)當t=﹣2+2
;(2)當t=3時,點D落在拋物線上;(3)當t=﹣2+2![]() 、t=8+4
、t=8+4![]() 時,以A、B、D為頂點的三角形與△PEB相似.
時,以A、B、D為頂點的三角形與△PEB相似.
【解析】試題分析:(1)根據題意利用待定系數法求出函數解析式,從而得到對稱軸;(2)根據題意得出點M的坐標,根據旋轉的性質得出點E和點B的坐標,從而得到點D的坐標,然后求出t的值;(3)分0<t<8和t>8兩種情況,每種情況分兩種情況進行討論計算,得出t的值.
試題解析:(1)由題得, ,解得
,解得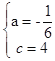 .
.
![]() 拋物線的解析式為:
拋物線的解析式為: ![]() ,它的對稱軸為:
,它的對稱軸為: ![]()
(2)由題意得: ![]() ,
, ![]() .
.
![]() 是
是![]() 繞點P順時針旋轉90°而得,
繞點P順時針旋轉90°而得, ![]()
![]() ,
, ![]() .從而有
.從而有![]() .
.
假設![]() 在拋物線上,有
在拋物線上,有![]() , 解得
, 解得![]()
∵![]() ,即當
,即當![]() 時,點D落在拋物線上.
時,點D落在拋物線上.
(3)①當![]() 時,如圖,
時,如圖,
![]() ,
,
(1)若△![]() ∽△ADB,此時
∽△ADB,此時![]() ,有:
,有: ![]() , ,即
, ,即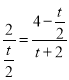 ,
,
化簡得![]() ,此時
,此時![]() 無解。
無解。
若△![]() ∽△ADB, 此時
∽△ADB, 此時![]() ,有:
,有: ![]() , ,即
, ,即 ,
,
化簡得: ![]() ,關于
,關于![]() 的一元二次方程的判別式
的一元二次方程的判別式![]() ,
,
由求根公式得:![]()
![]() ,
, ![]() 。
。
②當![]() 時,如圖②,若△POA∽△ADB
時,如圖②,若△POA∽△ADB![]()
(1)若△![]() ∽△ADB,此時
∽△ADB,此時![]() ,有:
,有:
![]() ,即
,即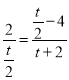 ,化簡得
,化簡得![]() ,解得
,解得![]() (負根舍去)。
(負根舍去)。
(2)若△![]() ∽△ADB,同理得此時
∽△ADB,同理得此時![]() 無解。
無解。
綜合上述:當![]() 、
、![]() 時,以A、B、D為頂點的三角形與△PEB相似。
時,以A、B、D為頂點的三角形與△PEB相似。


 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案科目:初中數學 來源: 題型:
【題目】自2009年起,每年的11月11日是Tmall一年一度全場大促銷的日子.某服飾店對某商品推出促銷活動:雙十一當天,買兩件等值的商品可在每件原價減50元的基礎上,再打八折;如果單買,則按原價購買.
(1)妮妮看中兩件原價都是300元的此類商品, 則在雙十一當天,購買這兩件商品總共需要多少錢?
(2)熊熊購買了兩件等值的此類商品后, 發現比兩件一起按原價六折購買便宜. 若這兩件等值商品的價格都是大于196的整數, 則原價可能是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面坐標坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的變換點
的變換點![]() 的坐標定義如下:當
的坐標定義如下:當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() ;當
;當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() .
.
已知點![]() ,點
,點![]() ,點
,點![]() .
.
(![]() )點
)點![]() 的變換點
的變換點![]() 的坐標是__________.
的坐標是__________.
點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,
,![]() ,則
,則![]() __________.
__________.
(![]() )點
)點![]() 的變換點為
的變換點為![]() ,隨著
,隨著![]() 的變化,點
的變化,點![]() 會運動起來,請在備用圖(
會運動起來,請在備用圖(![]() )中畫出點
)中畫出點![]() 的運動路徑.
的運動路徑.
(![]() )若
)若![]() 是等腰三角形,請直接寫出此時
是等腰三角形,請直接寫出此時![]() 的值:__________.
的值:__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,若點A(﹣2,n),B(1,﹣2)是一次函數y=kx+b的圖象和反比例函數y=![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求反比例函數和一次函數的解析式;
(2)求直線AB與x軸的交點C的坐標;
(3)求點O到直線AB的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數y=(2m+4)x,求:
(1)m為何值時,函數圖象經過第一、三象限?
(2)m為何值時,y隨x的增大而減小?
(3)m為何值時,點(1,3)在該函數的圖象上?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com