
【題目】在平面坐標坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的變換點
的變換點![]() 的坐標定義如下:當
的坐標定義如下:當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() ;當
;當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() .
.
已知點![]() ,點
,點![]() ,點
,點![]() .
.
(![]() )點
)點![]() 的變換點
的變換點![]() 的坐標是__________.
的坐標是__________.
點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,
,![]() ,則
,則![]() __________.
__________.
(![]() )點
)點![]() 的變換點為
的變換點為![]() ,隨著
,隨著![]() 的變化,點
的變化,點![]() 會運動起來,請在備用圖(
會運動起來,請在備用圖(![]() )中畫出點
)中畫出點![]() 的運動路徑.
的運動路徑.
(![]() )若
)若![]() 是等腰三角形,請直接寫出此時
是等腰三角形,請直接寫出此時![]() 的值:__________.
的值:__________.

【答案】(![]() )
)![]() ;
;![]() .(
.(![]() )點
)點![]() 的運動路徑見解析.(
的運動路徑見解析.(![]() )見解析.
)見解析.
【解析】試題分析:
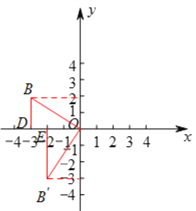
(1)①按照變換點的定義寫出A′的坐標即可;②按照變換點的定義根據點B的坐標寫出點B′的坐標,如圖,過點B作BD⊥x軸于點D,過點B′作B′E⊥x軸于點E,則由已知易證△BDO≌△OEB′,從而可證得∠BOD=∠OB′E,結合∠OB′E+∠EOB′=90°,即可證得∠BOB′=90°;
(2)①由變換點的定義可得,當n<2時,點C(2,n)的變換點的坐標是(-2,n);②當![]() 時,點C(2,n)的變換點的坐標是(-n,2),由此即可畫出點C的運動路線;
時,點C(2,n)的變換點的坐標是(-n,2),由此即可畫出點C的運動路線;
(3)由題意可知:![]() ,
,![]() ,連接
,連接![]() ,以
,以![]() 為圓心,
為圓心,![]() 長度為半徑作圓,交點
長度為半徑作圓,交點![]() 的運動路徑于點
的運動路徑于點![]() ;以
;以![]() 為圓心,
為圓心,![]() 長為半徑作圓,交點
長為半徑作圓,交點![]() 的運動路徑于點
的運動路徑于點![]() ,
,![]() ;作線段
;作線段![]() 的垂直平分線,交點
的垂直平分線,交點![]() 的運動路徑于點
的運動路徑于點![]() ,
,![]() ;如圖所示,
;如圖所示,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均為所求點
均為所求點![]() 的位置,再根據已知條件計算出對應的n的值即可.
的位置,再根據已知條件計算出對應的n的值即可.
試題解析:
(![]() )∵
)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
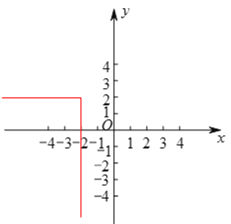
(![]() )點
)點![]() 的運動路徑如圖所示:
的運動路徑如圖所示:
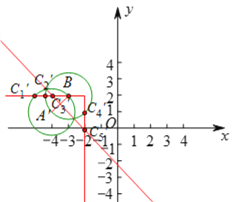
(![]() )如圖:
)如圖:![]() ,
,![]() ,連接
,連接![]() ,
,
以![]() 為圓心,
為圓心,![]() 長度為半徑作圓,交點
長度為半徑作圓,交點![]() 的運動路徑于點
的運動路徑于點![]() ,
,
以![]() 為圓心,
為圓心,![]() 長為半徑作圓,交點
長為半徑作圓,交點![]() 的運動路徑于點
的運動路徑于點![]() ,
,![]() ,
,
作線段![]() 的垂直平分線,交點
的垂直平分線,交點![]() 的運動路徑于點
的運動路徑于點![]() ,
,![]() ,
,
如圖所示,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均為所求點
均為所求點![]() 的位置,
的位置,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 為等腰直角三角形,
為等腰直角三角形,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
綜上所述,![]() 的值是
的值是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
【題目】在一次中學生田徑運動會上,根據參加男子跳高初賽的運動員的成績(單位:m),繪制出如下兩幅統計圖.請根據相關信息,解答下列問題:

(1)扇形統計圖中a= ,初賽成績為1.70m所在扇形圖形的圓心角為
(2)補全條形統計圖;
(3)這組初賽成績的眾數是 m,中位數是 ;
(4)根據這組初賽成績確定8人進入復賽,那么初賽成績為1.60m的運動員楊強能否進入復賽?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=ax2+![]() x+c過點A(0,4)和C(8,0),P(t,0)是x軸正半軸上的一個動點,M是線段AP的中點,將線段MP繞點P順時針旋轉90°得線段PB.過點B作x軸的垂線、過點A作y軸的垂線,兩直線相交于點D.
x+c過點A(0,4)和C(8,0),P(t,0)是x軸正半軸上的一個動點,M是線段AP的中點,將線段MP繞點P順時針旋轉90°得線段PB.過點B作x軸的垂線、過點A作y軸的垂線,兩直線相交于點D.
(1)求此拋物線的對稱軸;
(2)當t為何值時,點D落在拋物線上?
(3)是否存在t,使得以A、B、D為頂點的三角形與△PEB相似?若存在,求此時t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
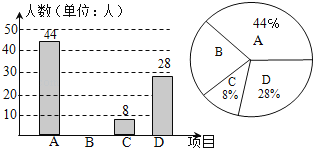
【題目】我區積極開展“體育大課間”活動,引導學生堅持體育鍛煉.某校根據實際情況,決定主要開設A:乒乓球,B:籃球,C:跑步,D:足球四種運動項目.為了解學生最喜歡哪一種項目,隨機抽取了部分學生進行調查,并將調查結果繪制成如下統計圖.請你結合圖中信息解答下列問題:
(1)求樣本中最喜歡B項目的人數百分比和其所在扇形圖中的圓心角的度數;
(2)請把條形統計圖補充完整;
(3)已知該校有1000人,請根據樣本估計全校最喜歡足球的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D在⊙O的直徑AB的延長線上,點C在⊙O上,AC=CD,∠ACD=120°.
(1)求證:CD是⊙O的切線;
(2)若⊙O的半徑為2,求圖中陰影部分的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com