Question

【題目】菱形ABCD在平面直角坐標系中的位置如圖所示，對角線AC與BD的交點E恰好在y軸上，過點D和BC的中點H的直線交AC于點F，線段DE，CD的長是方程x2﹣9x+18=0的兩根，請解答下列問題：

（1）求點D的坐標；

（2）若反比例函數y=（k≠0）的圖象經過點H，則k=　 　；

（3）點Q在直線BD上，在直線DH上是否存在點P，使以點F，C，P，Q為頂點的四邊形是平行四邊形？若存在，請直接寫出點P的坐標；若不存在，請說明理由．

Answer 1

【答案】（1）（﹣，3）（2） （3）（，）或（﹣，5）或（，﹣）

【解析】

（1）由線段DE，CD的長是方程x2﹣9x+18=0的兩根，且CD＞DE，可求出CD、DE的長，由四邊形ABCD是菱形，利用菱形的性質可求得D點的坐標.

(2)由（1）可得OB、CM，可得B、C坐標，進而求得H點坐標，由反比例函數y=（k≠0）的圖象經過點H，可求的k的值;

(3)分別以CF為平行四邊形的一邊或者為對角線的情形進行討論即可.

（1）x2﹣9x+18=0，

（x﹣3）（x﹣6）=0，

x=3或6，

∵CD＞DE，

∴CD=6，DE=3，

∵四邊形ABCD是菱形，

∴AC⊥BD，AE=EC==3，

∴∠DCA=30°，∠EDC=60°，

Rt△DEM中，∠DEM=30°，

∴DM=DE=，

∵OM⊥AB，

∴S菱形ABCD=ACBD=CDOM，

∴=6OM，OM=3，

∴D（﹣，3）；

（2）∵OB=DM=，CM=6﹣=，

∴B（，0），C（，3），

∵H是BC的中點，

∴H（3，），

∴k=3×=；

故答案為：；

（3）

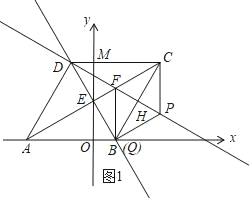
①∵DC=BC，∠DCB=60°，

∴△DCB是等邊三角形，

∵H是BC的中點，

∴DH⊥BC，

∴當Q與B重合時，如圖1，四邊形CFQP是平行四邊形，

∵FC=FB，

∴∠FCB=∠FBC=30°，

∴∠ABF=∠ABC﹣∠CBF=120°﹣30°=90°，

∴AB⊥BF，CP⊥AB，

Rt△ABF中，∠FAB=30°，AB=6，

∴FB=2=CP，

∴P（，）；

②

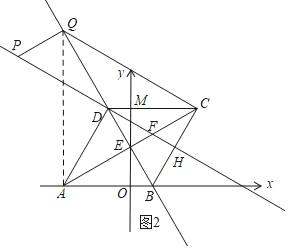
如圖2，∵四邊形QPFC是平行四邊形，

∴CQ∥PH，

由①知：PH⊥BC，

∴CQ⊥BC，

Rt△QBC中，BC=6，∠QBC=60°，

∴∠BQC=30°，

∴CQ=6，

連接QA，

∵AE=EC，QE⊥AC，

∴QA=QC=6，

∴∠QAC=∠QCA=60°，∠CAB=30°，

∴∠QAB=90°，

∴Q（﹣，6），

由①知：F（，2），

由F到C的平移規律可得P到Q的平移規律，則P（﹣﹣3，6﹣），即P（﹣，5）；

③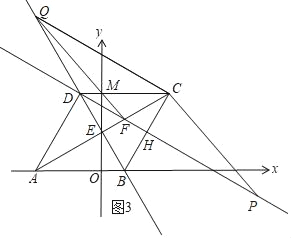

如圖3，四邊形CQFP是平行四邊形，

同理知：Q（﹣，6），F（，2），C（，3），

∴P（，﹣）；

綜上所述，點P的坐標為：（，）或（﹣，5）或（，﹣）．