
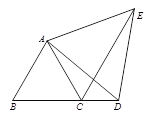
【題目】如圖,△ABC為等邊三角形,D為BC延長線上的一點,以AD為邊向形外作等邊△ADE,連接CE.(1) 求證:△ACE≌△ABD;
(2) 在點D運動過程中,∠DCE的度數是否發生變化?若不變化,求它的度數;若變化,說明理由;
(3) 若∠BAE=150°,△ABD的面積為6,求四邊形ACDE的面積.
備用圖
【答案】(1)證明見解析;(2)不發生變化,理由見解析;(3)12
【解析】試題分析:(1)易證AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,即可求得∠BAD=∠CAE,由全等三角形的判定SAS,證明△ABD≌△ACE;
(2)根據(1)知△ACE≌△ABD,然后根據全等三角形的性質和等邊三角形性質,得出∠DCE=60°,得出不發生變化;
(3)根據(1)的結論,由∠BAE=150°,得到△ACE,△DCE,△ABD的面積相等,從而求出四邊形的面積.
試題解析:(1) ∵△ABC為等邊三角形,△ADE為等邊三角形,∴∠ABC=∠ACB=60°,∠BAC=∠DAE=60°,AB=AC,AD=AE,∴∠BAC+∠DAC=∠DAC+∠DAE,即∠BAD=∠CAE.在△ACE與△ABD中,AB=AC,∠BAD=∠CAE,AD=AE,∴△ACE≌△ABD;
(2) 在點D運動過程中,∠DCE的度數不發生變化.理由如下:由(1)知:△ACE≌△ABD,∴∠ABC=∠ACE=60°.∵∠ACB=60°,∴∠ACD=120°,∠DCE=60°,∴在點D運動過程中,∠DCE的度數不發生變化.
(3)∵△ABC和△ADE是等邊三角形
∴∠BAC=∠DAE=60°
∵∠BAE=150°
∴∠CAD=30°,∠BAD=90°,
∴∠BAD=30°
即△ACE≌△DCE
∵△ABD≌△ACE
∴四邊形ACDE的面積=2△ACD的面積=2△ABD的面積=2×6=12.


科目:初中數學 來源: 題型:
【題目】霧霾已經成為時下最普遍與敏感的話題.某市記者為了了解“霧霾天氣的主要成因”,隨機調查了該市部分市民,并對調查結果進行整理,繪制了尚不完整的統計圖表.
級別 | 觀 點 | 頻數(人數) |
A | 大氣氣壓低,空氣不流動 | 80 |
B | 地面灰塵大,空氣濕度低 | m |
C | 汽車尾氣排放 | n |
D | 工廠造成的污染 | 120 |
E | 其他 | 60 |

請根據圖表中提供的信息解答下列問題:
(1)填空:m= ,n= ,扇形統計圖中E組所占的百分比為 %;
(2)若該市人口約有100萬人,請你估計其中持D組“觀點”的市民人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種襯衫因換季打折出售,如果按原價的六折出售,那么每件賠本40元;按原價的九折出售,那么每件盈利20元,則這種襯衫的原價是( )
A.160元B.180元C.200元D.220元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一個自然數所有數位上的數字先平方再求和得到一個新數,叫做第一次運算,再把所得新數所有數位上的數字先平方再求和又將得到一個新數,叫做第二次運算,……如此重復下去,若最終結果為1,我們把具有這種特征的自然數稱為“快樂數”.例如:
![]() ,
,
![]()
所以32和70都是“快樂數”.
(1)最小的兩位“快樂數”是 ;
(2)證明19是“快樂數”;
(3)若一個三位“快樂數”經過兩次運算后結果為1,把這個三位“快樂數”與它的各位上的數字相加所得的和被8除余數是2,求出這個“快樂數” .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠MON=30°,點A1、A2、A3…在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,從左起第1個等邊三角形的邊長記為a1,第2個等邊三角形的邊長記為a2,以此類推.若OA1=1,則a2015=( )
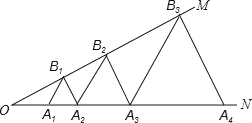
A. 22013 B. 22014 C. 22015 D. 22016
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究:如圖①,在△ABC中,AB=AC,∠ABC=60°,延長BA至點D,延長CB至點E,使BE=AD,連結CD,AE,求證:△ACE≌△CBD.
應用:如圖②,在菱形ABCF中,∠ABC=60°,延長BA至點D,延長CB至點E,使BE=AD,連結CD,EA,延長EA交CD于點G,求∠CGE的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com