【題目】某市種植某種綠色蔬菜，全部用來出口．為了擴大出口規模，該市決定對這種蔬菜的種植實行政府補貼，規定每種植﹣畝這種蔬菜一次性補貼菜農若干元．經調查，種植畝數y（畝）與補貼數額x（元）之間大致滿足如圖1所示的一次函數關系．隨著補貼數額x的不斷增大，出口量也不斷增加，但每畝蔬菜的收益z（元）會相應降低，且z與x之間也大致滿足如圖2所示的一次函數關系．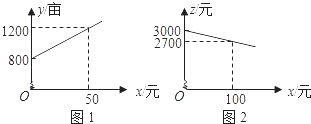 
（1）在政府未出臺補貼措施前，該市種植這種蔬菜的總收益額為多少？
（2）分別求出政府補貼政策實施后，種植畝數y和每畝蔬菜的收益z與政府補貼數額x之間的函數關系式；
（3）要使全市這種蔬菜的總收益w（元）最大，政府應將每畝補貼數額x定為多少？并求出總收益w的最大值．
【答案】
（1）解：政府沒出臺補貼政策前，這種蔬菜的收益額為3000×800=2400000（元）
（2）解：設種植畝數y和每畝蔬菜的收益z與政府補貼數額x之間的函數關系式分別為：
y=kx+800，z=k1x+3000，
分別把點（50，1200），（100，2700）代入得，
50k+800=1200，100k1+3000=2700，
解得：k=8，k1=﹣3，
種植畝數與政府補貼的函數關系為：y=8x+800
每畝蔬菜的收益與政府補貼的函數關系為z=﹣3x+3000（x＞0）
（3）解：由題意：
w=yz=（8x+800）（﹣3x+3000）
=﹣24x2+21600x+2400000
=﹣24（x﹣450）2+7260000，
∴當x=450，即政府每畝補貼450元時，總收益額最大，為7260000元
【解析】（1）根據題意可知直接計算這種蔬菜的收益額為3000×800=2400000（元）；（2）設種植畝數y和每畝蔬菜的收益z與政府補貼數額x之間的函數關系式分別為：y=kx+800，z=k1x+3000，并根據圖象上點的坐標利用待定系數法求函數的解析式即可；（3）表示出蔬菜的總收益w（元）與x之間的關系式，w=﹣24x2+21600x+2400000，利用二次函數最值問題求最大值．
科目：初中數學 來源： 題型：
【題目】今年是第39個植樹節，我們提出了“追求綠色時尚，走向綠色文明”的倡議．某校為積極響應這一倡議，立即在八、九年級開展征文活動，校團委對這兩個年級各班內的投稿情況進行統計，并制成了如圖所示的兩幅不完整的統計圖．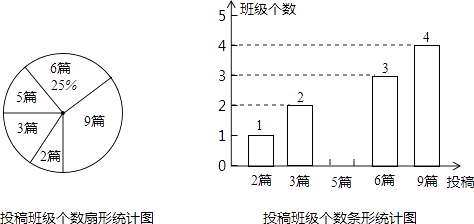 
（1）求扇形統計圖中投稿3篇的班級個數所對應的扇形的圓心角的度數．
（2）求該校八、九年級各班在這一周內投稿的平均篇數，并將該條形統計圖補充完整．
（3）在投稿篇數最多的4個班中，八、九年級各有兩個班，校團委準備從這四個班中選出兩個班參加全校的表彰會，請你用列表法或畫樹狀圖的方法求出所選兩個班正好不在同一年級的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
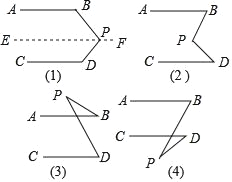
【題目】如圖（1），AB∥CD，試求∠BPD與∠B、∠D的數量關系，說明理由．
（1）填空：
解：過點P作EF∥AB，
∴∠B+∠BPE=180°
∵AB∥CD，EF∥AB
∴ （如果兩條直線都和第三條直線平行，那么這兩條直線也互相平行）
∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
（2）依照上面的解題方法，觀察圖（2），已知AB∥CD，猜想圖中的∠BPD與∠B、∠D的數量關系，并說明理由．
（3）觀察圖（3）和（4），已知AB∥CD，直接寫出圖中的∠BPD與∠B、∠D的數量關系，不用說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，將邊長為1的正方形ABCD壓扁為邊長為1的菱形ABCD．在菱形ABCD中，∠A的大小為α，面積記為S．
（1）請補全下表：
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
（2）填空：
由（1）可以發現正方形在壓扁的過程中，菱形的面積隨著∠A大小的變化而變化，不妨把菱形的面積S記為S(α)．例如：當α＝30°時，
；當α＝135°時，
．由上表可以得到
( ______°)；
( ______°)，…，由此可以歸納出
．
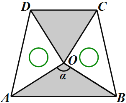
（3） 兩塊相同的等腰直角三角板按如圖的方式放置，AD＝
，∠AOB＝α，試探究圖中兩個帶陰影的三角形面積是否相等，并說明理由（注：可以利用（2）中的結論）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某研究機構經過抽樣調查，發現當地1500個老年人的養老模式主要有A，B，C，D，E五種，統計結果如圖，那么下列說法不正確的是（ ）
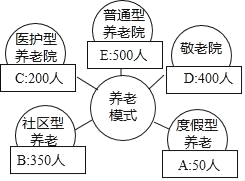
A. 選擇A型養老的頻率是
B. 可以估計當地30000個老年人中有8000人選擇C型養老
C. 樣本容量是1500
D. 總體是當地1500個老年人的養老模式
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在不透明的袋子中有黑棋子10枚和白棋子若干（它們除顏色外都相同），現隨機從中摸出10枚記下顏色后放回，這樣連續做了10次，記錄了如下的數據：
次數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋數 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根據以上數據，解答下列問題：
（I）直接填空：第10次摸棋子摸到黑棋子的頻率為 ；
（Ⅱ）試估算袋中的白棋子數量．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】鐵路貨運調度站有A、B兩個信號燈，在燈這旁停靠著甲、乙、丙三列火車．它們中最長的車長與居中車長之差等于居中車長與最短車長之差，其中乙車的車長居中，最開始的時候，甲、丙兩車車尾對齊，且車尾正好位于A信號燈處，而車頭則沖著B信號燈的方向，乙車的車尾則位于B信號燈處，車頭則沖著A的方向，現在，三列火車同時出發向前行駛，3秒之后三列火車的車頭恰好相遇，再過9秒，甲車恰好超過丙車，而丙車也正好完全和乙車錯開，請問：甲乙兩車從車頭相遇直到完全錯開一共用了_____秒鐘．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
