
【題目】定義:若![]() ,則稱
,則稱![]() 與
與![]() 是關(guān)于1的平衡數(shù).
是關(guān)于1的平衡數(shù).
(1)3與______是關(guān)于1的平衡數(shù);![]() 與______是關(guān)于1的平衡數(shù)(用含
與______是關(guān)于1的平衡數(shù)(用含![]() 的代數(shù)式表示).
的代數(shù)式表示).
(2)若![]() ,
,![]() ,判斷
,判斷![]() 與
與![]() 是否是關(guān)于1的平衡數(shù),并說明理由.
是否是關(guān)于1的平衡數(shù),并說明理由.
(3)若![]() 與-1是關(guān)于1的平衡數(shù),
與-1是關(guān)于1的平衡數(shù),![]() 與-2是關(guān)于1的平衡數(shù),求與
與-2是關(guān)于1的平衡數(shù),求與![]() 關(guān)于1的平衡數(shù).
關(guān)于1的平衡數(shù).
【答案】(1)-1,x-3;(2)是,理由見解析;(3)![]() 關(guān)于1的平衡數(shù)是-6或10.
關(guān)于1的平衡數(shù)是-6或10.
【解析】
(1)根據(jù)平衡數(shù)的定義,可得3與-1是關(guān)于1的平衡數(shù),5-x與x-3是關(guān)于1的平衡數(shù);
(2)判定a、b是不是關(guān)于1的平衡數(shù),只需要看a+b是不是等于2即可,把這兩個數(shù)相加化簡即得;
(3)根據(jù)平衡數(shù)的定義,列出方程式求解,分情況討論,最后把x、y代入所求式子即可.
由題意知,![]() ,則稱
,則稱![]() 與
與![]() 是關(guān)于1的平衡數(shù),即
是關(guān)于1的平衡數(shù),即![]() 、
、![]() 兩數(shù)和為2,
兩數(shù)和為2,
(1)∵2-3=-1,2-(5-x)=x-3,
∴3與-1是關(guān)于1的平衡數(shù),5-x與x-3是關(guān)于1的平衡數(shù),
故答案為:-1,x-3;
(2)∵![]()
![]()
∴![]() 與
與![]() 是關(guān)于1的平衡數(shù),
是關(guān)于1的平衡數(shù),
故答案為:是;
(3)∵x-1=2, ![]() -2=2,
-2=2,
∴x=3,y=![]() 2,
2,
當(dāng)x=3,y=2時,![]() =8,8關(guān)于1的平衡數(shù)是2-8=-6,
=8,8關(guān)于1的平衡數(shù)是2-8=-6,
當(dāng)x=3,y=-2時,![]() =-8,-8關(guān)于1的平衡數(shù)是2-(-8)=10,
=-8,-8關(guān)于1的平衡數(shù)是2-(-8)=10,
綜上所述,![]() 關(guān)于1的平衡數(shù)是-6或10,
關(guān)于1的平衡數(shù)是-6或10,
故答案為:-6或10.


 學(xué)練快車道快樂假期寒假作業(yè)系列答案
學(xué)練快車道快樂假期寒假作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AC,BD相交于點(diǎn)O,AC平分∠DCB,CD⊥AD,∠ACD=45°,∠BAC=60°.
(1)證明:AD∥BC;
(2)求∠EAD的度數(shù);
(3)求證:∠AOB=∠DAC +∠CBD

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
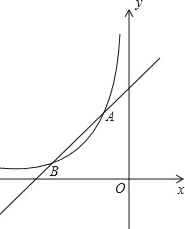
【題目】如圖,函數(shù)![]() (x<0)與y=ax+b的圖象交于點(diǎn)A(﹣1,n)和點(diǎn)B(﹣2,1).
(x<0)與y=ax+b的圖象交于點(diǎn)A(﹣1,n)和點(diǎn)B(﹣2,1).
(1)求k,a,b的值;
(2)直線x=m與![]() (x<0)的圖象交于點(diǎn)P,與y=﹣x+1的圖象交于點(diǎn)Q,當(dāng)∠PAQ>90°時,直接寫出m的取值范圍.
(x<0)的圖象交于點(diǎn)P,與y=﹣x+1的圖象交于點(diǎn)Q,當(dāng)∠PAQ>90°時,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1在△ABC中,∠ACB=90°,AC=BC,直線MN經(jīng)過點(diǎn)C,且AD⊥MN于點(diǎn)D,BE⊥MN于點(diǎn)E.
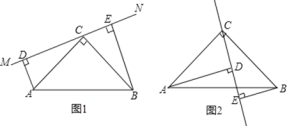
(1)求證:①△ADC≌△CEB;②DE=AD+BE.
(2)當(dāng)直線MN繞點(diǎn)C旋轉(zhuǎn)到圖2的位置時,DE、AD、BE又怎樣的關(guān)系?并加以證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)問題進(jìn)行證明:
(1)已知:如圖,在正方形ABCD中,點(diǎn)E在邊CD上,AQ⊥BE于點(diǎn)Q,DP⊥AQ于點(diǎn)P,求證:AP=BQ.
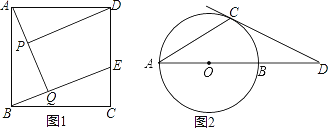
(2)如圖,已知AB是⊙O的直徑,AC是⊙O的弦,過點(diǎn)C的切線交AB的延長線于點(diǎn)D且∠A=∠D.求∠D的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)軸上![]() 點(diǎn)表示的數(shù)是
點(diǎn)表示的數(shù)是![]() ,
,![]() 點(diǎn)表示的數(shù)是
點(diǎn)表示的數(shù)是![]() ,則線段
,則線段![]() 的長表示為
的長表示為![]() .例如:數(shù)軸上
.例如:數(shù)軸上![]() 點(diǎn)表示的數(shù)是5,
點(diǎn)表示的數(shù)是5,![]() 點(diǎn)表示的數(shù)是2,則線段
點(diǎn)表示的數(shù)是2,則線段![]() 的長表示為
的長表示為![]() .
.
(1)點(diǎn)![]() 表示的數(shù)是3,線段
表示的數(shù)是3,線段![]() 的長可表示為______.
的長可表示為______.
(2)若![]() ,
,![]() ______.
______.
(3)數(shù)軸上的任意一點(diǎn)![]() 表示的數(shù)是
表示的數(shù)是![]() ,且
,且![]() 的最小值為5,若
的最小值為5,若![]() ,則
,則![]() 的值為______.
的值為______.
(4)如圖,在數(shù)軸上點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的右邊
的右邊![]() ,
,![]() ,若代數(shù)式
,若代數(shù)式![]() 與
與![]() 互為相反數(shù),求
互為相反數(shù),求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
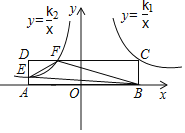
【題目】如圖,矩形ABCD的頂點(diǎn)A,B在x軸上,且關(guān)于y軸對稱,反比例函數(shù)y=![]() (x>0)的圖象經(jīng)過點(diǎn)C,反比例函數(shù)y=
(x>0)的圖象經(jīng)過點(diǎn)C,反比例函數(shù)y=![]() (x<0)的圖象分別與AD,CD交于點(diǎn)E,F(xiàn),若S△BEF=7,k1+3k2=0,則k1等于_____.
(x<0)的圖象分別與AD,CD交于點(diǎn)E,F(xiàn),若S△BEF=7,k1+3k2=0,則k1等于_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
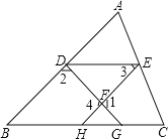
【題目】如圖:點(diǎn)D、E、H、G分別在△ABC的邊上DE∥BC,∠3=∠B,DG、EH交于點(diǎn)F.求證:∠1+∠2=180°
證明:(請將下面的證明過程補(bǔ)充完整)
∵DE∥BC(已知)
∴∠3=∠EHC(______)
∵∠3=∠B(已知)
∴∠B=∠EHC(______)
∴AB∥EH(______)
∴∠2+∠______=180°(______)
∵∠1=∠4(______)
∴∠1+∠2=180°(等量代換)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,已知AB=AC,D為∠BAC的角平分線上面一點(diǎn),連接BD,CD;如圖2,已知AB=AC,D、E為∠BAC的角平分線上面兩點(diǎn),連接BD,CD,BE,CE;如圖3,已知AB=AC,D、E、F為∠BAC的角平分線上面三點(diǎn),連接BD,CD,BE,CE,BF,CF;…,依次規(guī)律,第n個圖形中有全等三角形的對數(shù)是_________.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com