
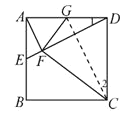
【題目】如圖,在正方形![]() 中,點
中,點![]() 為
為![]() 邊的中點,點
邊的中點,點![]() 在
在![]() 上,
上,![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .正確的是( ).
.正確的是( ).

A.①②B.①③C.①③④D.③④
【答案】C
【解析】
連接![]() .根據“HL”可證
.根據“HL”可證![]() ≌
≌![]() ,利用全等三角形的對應邊相等,可得
,利用全等三角形的對應邊相等,可得![]() ,據此判斷①;根據“
,據此判斷①;根據“![]() ”可證
”可證![]() ≌
≌![]() ,可得
,可得![]() ,從而可得
,從而可得![]() ,據此判斷②;由(2)知
,據此判斷②;由(2)知![]() ,可證
,可證![]() ,據此判斷③;根據兩角分別相等的兩個三角形相似,可證
,據此判斷③;根據兩角分別相等的兩個三角形相似,可證![]() ∽
∽![]() ∽
∽![]() ,可得
,可得![]() , 從而可得
, 從而可得![]() ,據此判斷④.
,據此判斷④.
解:(1)連接![]() . 如圖所示:
. 如圖所示:
∵四邊形ABCD是正方形,
∴∠ADC=90°,
∵FG⊥FC,
∴∠GFC=90°,
在Rt△CFG與Rt△CDG中,![]()
∴![]() ≌
≌![]() .
.
∴![]() ...①正確.
...①正確.
(2)由(1),![]() 垂直平分
垂直平分![]() .∴∠EDC+∠2=90°,
.∴∠EDC+∠2=90°,
∵∠1+∠EDC=90°,
∴![]() .
.
∵四邊形ABCD是正方形,
∴AD=DC=AB,∠DAE=∠CDG=90°,
∴![]() ≌
≌![]() .
.
∴![]() .
.
∵![]() 為
為![]() 邊的中點,
邊的中點,
∴![]() 為
為![]() 邊的中點.
邊的中點.
∴![]() .∴②錯誤.
.∴②錯誤.
(3)由(2),得![]() . ∴
. ∴![]() .③正確.
.③正確.
(4)由(3),可得![]() ∽
∽![]() ∽
∽![]() . ∴
. ∴ ![]()
∴![]() . ∴④正確.
. ∴④正確.
故答案為:C.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:
【題目】在菱形ABCD中,點P是BC邊上一點,連接AP,點E,F是AP上的兩點,連接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求證:(1)△ABF≌△DAE;
(2)DE=BF+EF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中 xOy 中,對于⊙C及⊙C內一點 P,給出如下定義:若存在過點 P 的直線 l,使得它與⊙C 相交所截得的弦長為![]() ,則稱點 P 為⊙C的“k-近內點”.
,則稱點 P 為⊙C的“k-近內點”.
(1)已知⊙O的半徑為 4,
①在點中![]() ,⊙O的“4-近內點”是______________;
,⊙O的“4-近內點”是______________;
②點 P 在直線y=![]() x上,若點 P 為⊙O的“4-近內點”,則點 P 的縱坐標y的取值范圍是____________;
x上,若點 P 為⊙O的“4-近內點”,則點 P 的縱坐標y的取值范圍是____________;
(2)⊙C的圓心為(-1,0),半徑為 3,直線![]() x 軸,y 軸分別交于 M,N,若線段 MN 上存在⊙C的 “2
x 軸,y 軸分別交于 M,N,若線段 MN 上存在⊙C的 “2![]() -近內點”,則 b 的取值范圍是____________.
-近內點”,則 b 的取值范圍是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
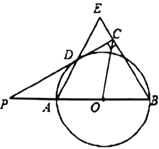
【題目】如圖,已知AB是![]() 的直徑,點P在BA的延長線上,PD切
的直徑,點P在BA的延長線上,PD切![]() 于點D,過點B作
于點D,過點B作![]() ,交PD的延長線于點C,連接AD并延長,交BE于點E.
,交PD的延長線于點C,連接AD并延長,交BE于點E.
(Ⅰ)求證:AB=BE;
(Ⅱ)連結OC,如果PD=2![]() ,∠ABC=60°,求OC的長.
,∠ABC=60°,求OC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果專賣店5月份銷售芒果,采購價為10元![]() ,上旬售價是15元
,上旬售價是15元![]() ,每天可賣出450
,每天可賣出450![]() .市場調查反映:如調整單價,每漲價1元,每天要少賣出50
.市場調查反映:如調整單價,每漲價1元,每天要少賣出50![]() ;每降價1元,每天可多賣出150
;每降價1元,每天可多賣出150![]() .調整價格時也要兼顧顧客利益。
.調整價格時也要兼顧顧客利益。
(1)若專賣店5月中旬每天獲得毛利2400元,試求出是如何確定售價的.
(2)請你幫老板算一算,5月下旬如何確定售價每天獲得毛利最大,并求出最大毛利.
查看答案和解析>>
科目:初中數學 來源: 題型:
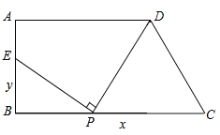
【題目】如圖:梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=6,在線段BC上任取一點P,連接DP,作射線PE⊥DP,PE與直線AB交于點E.
(1)試確定當CP=3時,點E的位置;
(2)若設CP=x,BE=y,試寫出y關于自變量x的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的布袋里有材質、形狀、大小完全相同的4個小球,它們的表面分別印有1、2、3、4四個數字(每個小球只印有一個數字),小華從布袋里隨機摸出一個小球,把該小球上的數字記為![]() ,小剛從剩下的3個小球中隨機摸出一個小球,把該小球上的數字記為
,小剛從剩下的3個小球中隨機摸出一個小球,把該小球上的數字記為![]() .
.
(1)若小華摸出的小球上的數字是2,求小剛摸出的小球上的數字是3的概率;
(2)利用畫樹狀圖或列表格的方法,求點![]() 在函數
在函數![]() 的圖象上的概率.
的圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司研發生產的560件新產品需要精加工后才能投放市場.現由甲、乙兩個工廠來加工生產,已知甲工廠每天加工生產的新產品件數是乙工廠每天加工生產新產品件數的1.5倍,并且加工生產240件新產品甲工廠比乙工廠少用4天.
(1)求甲、乙兩個工廠每天分別可加工生產多少件新產品?
(2)若甲工廠每天的加工生產成本為2.8萬元,乙工廠每天的加工生產成本為2.4萬元要使這批新產品的加工生產總成本不超過60萬元,至少應安排甲工廠加工生產多少天?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com