
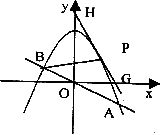
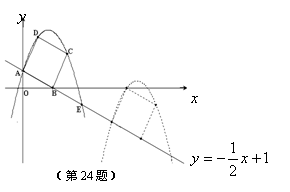
如圖,已知直線![]() 與拋物線
與拋物線![]() 交于A、B兩點.
交于A、B兩點.
(1)求A、B兩點的坐標;
(2)求線段AB的垂直平分線的解析式;
(3)如圖,取與線段AB等長的一根橡皮筋,端點分別固定在A、B兩處.用鉛筆拉著這根橡皮筋使筆尖P在直線AB上方的拋物線上移動,動點P將與A、B構成無數個三角形,這些三角形中是否存在一個面積最大的三角形?如果存在,求出最大面積,并指出此時P點的坐標;如果不存在,請簡要說明理由.


解:(1)依題意得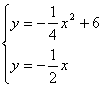 ,解
,解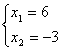 ;或
;或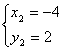 ,∴A(6,-3),B(-4,2),
,∴A(6,-3),B(-4,2),
(2)作AB的垂直平分線交![]() 軸,
軸,![]() 軸于C,D兩點,交AB于M.
軸于C,D兩點,交AB于M.
由(1)可知:OA=![]() 、OB=
、OB=![]() 。
。
∴AB=![]() 。∴
。∴![]() 。
。
過B作BE⊥![]() 軸,E為垂足。
軸,E為垂足。
由△BEO∽OMC,得:![]() ,
,
∴![]() ,同理:
,同理:![]() ,∴
,∴![]() ,
,![]() 。
。
設CD的解析式為![]() 。
。
∴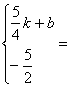 ∴
∴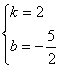
∴AB的垂直平分線的解析式為:![]()
(3)若存在點P使△APB的面積最大,則點P在與直線AB平行且和拋物線只有一個交點的直線![]() 上,并設該直線與
上,并設該直線與![]() 軸,
軸,![]() 軸交于G、H兩點。
軸交于G、H兩點。
∴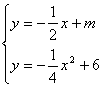
∴![]()
∵拋物線與直線只有一個交點,(可用![]() 轉換)
轉換)
∴![]() ,∴
,∴![]() 。∴
。∴![]() 。
。
在直線GH:![]() 中,
中,
∴![]() ,
,![]()
∴![]() 。設O到GH的距離為
。設O到GH的距離為![]() ,
,
∴![]() 。
。
∴![]() 。
。
∴![]()
∵AB∥GH,∴P到AB的距離等于O到GH的距離![]() 。
。
∴![]() 。
。



 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:初中數學 來源: 題型:
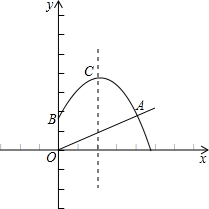 點C的坐標為(2,3.5).
點C的坐標為(2,3.5). 查看答案和解析>>
科目:初中數學 來源:中考必備’04全國中考試題集錦·數學 題型:044
如圖,已知拋物y=x2-ax+a+2與x軸交于A、B兩點,與y軸交于點D(0,8),直線DC平行于x軸,交拋物線于另一點C.動點P以每秒2個單位長度的速度從點C出發,沿C→D運動.同時、點Q以每秒1個單位長度的速度從點A出發,沿A→B運動.連結PQ、CB.設點P的運動時間為t秒.

(1)求a的值;
(2)當t為何值時,PQ平行于y軸;
(3)當四邊形PQBC的面積等于14時,求t的值.
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(福建龍巖卷)數學(解析版) 題型:解答題
在平面直角坐標系xoy中, 一塊含60°角的三角板作如圖擺放,斜邊 AB在x軸上,直角頂點C在y軸正半軸上,已知點A(-1,0).
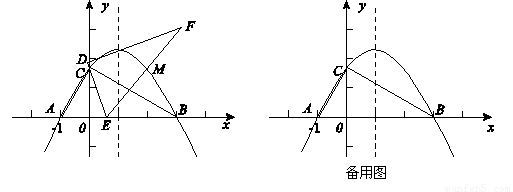
(1)請直接寫出點B、C的坐標:B( , )、C( , );并求經過A、B、C三點的拋物
線解析式;
(2)現有與上述三角板完全一樣的三角板DEF(其中∠EDF=90°,∠DEF=60°),把頂點E放在線段
AB上(點E是不與A、B兩點重合的動點),并使ED所在直線經過點C. 此時,EF所在直線與(1)中的拋物線交于第一象限的點M.
①設AE=x,當x為何值時,△OCE∽△OBC;
②在①的條件下探究:拋物線的對稱軸上是否存在點P使△PEM是等腰三角形,若存在,請求點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年廣西省貴港市九年級第一次教學質量監測數學卷 題型:解答題
(本題滿分12分)
如圖所示,在平面直角坐標系中,頂點為(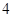 ,
,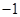 )的拋物線交
)的拋物線交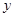 軸于
軸于 點,交
點,交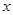 軸于
軸于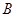 ,
,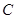 兩點(點
兩點(點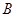 在點
在點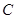 的左側),
已知
的左側),
已知 點坐標為(
點坐標為( ,
,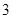 ).
).
(1)求此拋物線的解析式;
(2)過點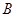 作線段
作線段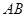 的垂線交拋物線于點
的垂線交拋物線于點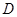 ,
,
如果以點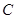 為圓心的圓與直線
為圓心的圓與直線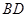 相切,請判斷拋物
相切,請判斷拋物
線的對稱軸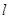 與⊙
與⊙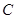 有怎樣的位置關系,并給出證明;
有怎樣的位置關系,并給出證明;
(3)已知點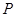 是拋物線上的一個動點,且位于
是拋物線上的一個動點,且位于 ,
,
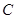 兩點之間,問:當點
兩點之間,問:當點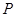 運動到什么位置時,
運動到什么位置時,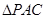 的
的
面積最大?并求出此時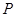 點的坐標和
點的坐標和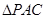 的最大面積.
的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
.如圖,已 知直線 ![]() 交坐標軸于
交坐標軸于![]() 兩點,以線段
兩點,以線段![]()
![]() 為邊向上作正方形
為邊向上作正方形![]() ,過點
,過點![]() 的拋物線與直線另一個交點為
的拋物線與直線另一個交點為![]() .
.
(1)請直接寫出點![]() 的坐標;
的坐標;
(2)求拋物線的解析式;
(3)若正方形以每秒![]() 個單位長度的速度沿射線
個單位長度的速度沿射線![]() 下滑,直至頂點
下滑,直至頂點![]() 落在x軸上時停止.設正方形落在
落在x軸上時停止.設正方形落在![]() 軸下方部分的面積為
軸下方部分的面積為![]() ,求
,求![]() 關于滑行時間
關于滑行時間![]() 的函數關系式,并寫出相應自變量
的函數關系式,并寫出相應自變量![]() 的取值范圍;
的取值范圍;
(4)在(3)的條件下,拋物線與正方形一起平移,同時停止,求拋物線上![]() 兩點間的拋物
兩點間的拋物
線弧所掃過的面積.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com