
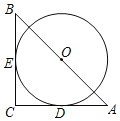
【題目】如圖,在Rt△ABC中,∠C=90°,AB=4![]() ,以AB的中點O為圓心作圓,圓O分別與AC、BC相切于點D、E兩點,則弧DE的長為__.
,以AB的中點O為圓心作圓,圓O分別與AC、BC相切于點D、E兩點,則弧DE的長為__.
【答案】π.
【解析】
連接OE,OD,根據切線的性質得到OE⊥BC,OD⊥AC,推出矩形OECD是正方形,得到CE=CD,∠EOD=90°,根據全等三角形的性質得到BE=OD,OE=AD,求得BE=OE=OD=AD,根據等腰直角三角形的性質得到AB=4![]() ,求得OE=OD=2,根據弧長公式即可得到結論.
,求得OE=OD=2,根據弧長公式即可得到結論.
連接OE,OD,
∵圓O分別與AC、BC相切于點D、E兩點,
∴OE⊥BC,OD⊥AC,
∵∠C=90°,
∴四邊形OECD是矩形,
∵OE=OD,
∴矩形OECD是正方形,
∴CE=CD,∠EOD=90°,
∴∠B+∠BOE=∠BOE+∠AOD=90°,
∴∠B=∠AOD,
∵∠BEO=∠ADO=90°,OB=OA,
∴△BOE≌△OAD(AAS),
∴BE=OD,OE=AD,
∴BE=OE=OD=AD,
∴∠B=∠A=45°,
∵AB=4![]() ,
,
∴OE=OD=2,
∴弧DE的長=![]() ,
,
故答案為:π.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】近幾年購物的支付方式日益增多,某數學興趣小組就此進行了抽樣調查.調查結果顯示,支付方式有:A微信、B支付寶、C現金、D其他,該小組對某超市一天內購買者的支付方式進行調查統計,得到如下兩幅不完整的統計圖.

請你根據統計圖提供的信息,解答下列問題:
(1)本次一共調查了多少名購買者?
(2)請補全條形統計圖;在扇形統計圖中A種支付方式所對應的圓心角為 度.
(3)若該超市這一周內有1600名購買者,請你估計使用A和B兩種支付方式的購買者共有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
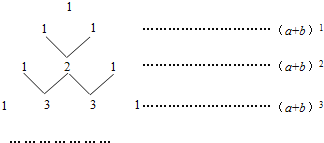
【題目】我國古代數學的許多發現都曾位居世界前列,其中“楊輝三角”就是一例.如圖,這個三角形的構造法則:兩腰上的數都是1,其余每個數均為其上方左、右兩數之和,它給出了(a+b)n(n為正整數)的展開式(按a的次數由大到小的順序排列)的系數規律.例如,在三角形中第三行的三個數1,2,1,恰好對應(a+b)2=a2+2ab+b2展開式中的系數;第四行的四個數1,3,3,1,恰好對應著(a+b)3=a3+3a2b+3ab2+b2展開式中的系數等.
(1)(a+b)n展開式中項數共有 項.
(2)寫出(a+b)5的展開式:(a+b)5= .
(3)利用上面的規律計算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中數學 來源: 題型:
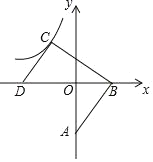
【題目】如圖,已知直線AB分別交x軸和y軸與B、A兩點,A(0,﹣3),B(2,0).
(1)求出直線AB的解析式;
(2)將線段AB平移至DC的位置,其D點在x軸的負半軸上,C點在反比例函數y=![]() 的圖象上,若S△BCD=18,則反比例函數解析式為____;
的圖象上,若S△BCD=18,則反比例函數解析式為____;
(3)設BC交y軸于P,求S△ABP.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一游客步行從賓館C出發,沿北偏東60°的方向行走到1000米的人民公園A處,參觀后又從A處沿正南方向行走一段距離到達位于賓館南偏東45°方向的凈業寺B處,如圖所示.
(1)求這名游客從人民公園到凈業寺的途中到賓館的最短距離;
(2)若這名游客以80米/分的速度從凈業寺返回賓館,那么他能在10分鐘內到達賓館嗎?請通過計算說明理由.(假設游客行走的路線均是沿直線行走的)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,點
,點![]() 沿
沿![]() 邊從點
邊從點![]() 開始向點
開始向點![]() 以每秒
以每秒![]() 個單位長度的速度運動;點
個單位長度的速度運動;點![]() 沿
沿![]() 邊從點
邊從點![]() 開始向點
開始向點![]() 以每秒
以每秒![]() 個單位長度的速度運動.如果
個單位長度的速度運動.如果![]() ,
,![]() 同時出發,用
同時出發,用![]() 秒表示運動的時間.
秒表示運動的時間.

請解答下列問題:
(1)當![]() 為何值時,
為何值時,![]() 是等腰直角三角形?
是等腰直角三角形?
(2)當![]() t為何值時,以點
t為何值時,以點![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?
相似?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了改善辦公條件,計劃從廠家購買![]() 兩種型號電腦.已知每臺
兩種型號電腦.已知每臺![]() 種型號電腦價格比每臺
種型號電腦價格比每臺![]() 種型號電腦價格多0.1萬元,且用10萬元購買
種型號電腦價格多0.1萬元,且用10萬元購買![]() 種型號電腦的數量與用8萬購買
種型號電腦的數量與用8萬購買![]() 種型號電腦的數量相同.
種型號電腦的數量相同.
(1)求![]() 兩種型號電腦每臺價格各為多少萬元?
兩種型號電腦每臺價格各為多少萬元?
(2)學校預計用不多于9.2萬元的資金購進這兩種電腦共20臺,其中![]() 種型號電腦至少要購進10臺,請問有哪幾種購買方案?
種型號電腦至少要購進10臺,請問有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
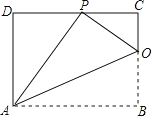
【題目】已知矩形ABCD的一條邊AD=8,將矩形ABCD折疊,使得頂點B落在CD邊上的P點處.如圖,已知折痕與邊BC交于點O,連接AP、OP、OA.
(1)求證:![]() ;
;
(2)若△OCP與△PDA的面積比為1:4,求邊AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com