
【題目】如圖,點![]() 在正方形
在正方形![]() 外,連接
外,連接![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于
于![]() ,若
,若![]() ,則下列結論不正確的是( )
,則下列結論不正確的是( )

A.![]() B.點
B.點![]() 到直線
到直線![]() 的距離為
的距離為![]()
C.![]() D.
D.![]()
【答案】B
【解析】
A、首先利用已知條件根據邊角邊可以證明△APD≌△AEB;
B、利用全等三角形的性質和對頂角相等即可解答;
C、由(1)可得∠BEF=90°,故BE不垂直于AE過點B作BP⊥AE延長線于P,由①得∠AEB=135°所以∠PEB=45°,所以△EPB是等腰Rt△,于是得到結論;
D、根據勾股定理和三角形的面積公式解答即可.
解:在正方形ABCD中,AB=AD,
∵AF⊥AE,
∴∠BAE+∠BAF=90°,
又∵∠DAF+∠BAF=∠BAD=90°,
∴∠BAE=∠DAF,
在△AFD和△AEB中,

∴△AFD≌△AEB(SAS),故A正確;

∵AE=AF,AF⊥AE,
∴△AEF是等腰直角三角形,
∴∠AEF=∠AFE=45°,
∴∠AEB=∠AFD=180°45°=135°,
∴∠BEF=135°45°=90°,
∴EB⊥ED,故C正確;
∵AE=AF=![]() ,
,
∴FE=![]() AE=2,
AE=2,
在Rt△FBE中,BE=![]() ,
,
∴S△APD+S△APB=S△APE+S△BPE,
=![]()
![]() ,故D正確;
,故D正確;
過點B作BP⊥AE交AE的延長線于P,
∵∠BEP=180°135°=45°,
∴△BEP是等腰直角三角形,
∴BP=![]() ,
,
即點B到直線AE的距離為![]() ,故B錯誤,
,故B錯誤,
故選:B.


科目:初中數學 來源: 題型:
【題目】探究學習:
(1)感知與填空
如圖,直線![]() .求證:
.求證:![]() .
.
閱讀下面的解答過程,并填上適當的理由.
解:延長![]() 交
交![]() 于
于![]() ,
,

∵![]() (已知),∴
(已知),∴![]() ( )
( )
∵![]() ( ),
( ),
∴![]() (等量代換)
(等量代換)
(2)應用與拓展
如圖,直線![]() .若
.若![]() ,
,![]() ,
,![]() ,則
,則![]() ______度.
______度.

(3)方法與實踐
如圖,直線![]() .請探究
.請探究![]() ,
,![]() 和
和![]() 之間有怎樣的關系,并證明你的結論.
之間有怎樣的關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組
請結合題意填空,完成本題的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在數軸上表示出來:
![]()
(4)原不等式維的解集為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三角形ABC(記作△ABC)在8×8方格中,位置如圖所示,A(﹣2,1),B(﹣1,4).
(1)請你在方格中建立直角坐標系,并寫出C點的坐標;
(2)把△ABC向上平移2個單位長度,再向右平移3個單位長度,請你畫出平移后的△A1B1C1,若△ABC內部一點P的坐標為(a,b),則點P的對應點P1的坐標是 .
(3)在x軸上存在一點D,使△DBC的面積等于3,則點D的坐標為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】網格中每一格的邊長為1個單位長度,已知四邊形ABCD的頂點均在網格的格點上.

(1)將四邊形ABCD進行平移,使點A移動到點D的位置,得到四邊形DB′C′D′,畫出平移后的圖形;
(2)根據(1)所畫的圖形,請指出圖中平行的線段;
(3)在(1)的基礎上,若∠BDC=65°,求∠B′D′C′的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形![]() 和正方形
和正方形![]() 中,邊
中,邊![]() 在邊
在邊![]() 上,
上,![]() 正方形
正方形![]() 繞點
繞點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]()
(1)如圖2,當![]() 時,求證:
時,求證:![]() ;
;
(2)在旋轉的過程中,設![]() 的延長線交直線
的延長線交直線![]() 于點
于點![]() .①如果存在某一時刻使得
.①如果存在某一時刻使得![]() ,請求出此時
,請求出此時![]() 的長;②若正方形
的長;②若正方形![]() 繞點
繞點![]() 按逆時針方向旋轉了
按逆時針方向旋轉了![]() ,求旋轉過程中,點
,求旋轉過程中,點![]() 運動的路徑長.
運動的路徑長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人進行羽毛球比賽,羽毛球飛行的路線為拋物線的一部分,如圖,甲在O點正上方1m的P處發出一球,羽毛球飛行的高度y(m)與水平距離x(m)之間滿足函數表達式y=a(x﹣4)2+h,已知點O與球網的水平距離為5m,球網的高度為1.55m.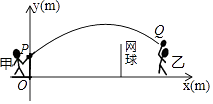
(1)當a=﹣ ![]() 時,①求h的值;
時,①求h的值;
②通過計算判斷此球能否過網.
(2)若甲發球過網后,羽毛球飛行到與點O的水平距離為7m,離地面的高度為 ![]() m的Q處時,乙扣球成功,求a的值.
m的Q處時,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了響應國家節能減排的號召,鼓勵市民節約用電,某市從2012年7月1日起,居民用電實行“一戶一表”的“階梯電價”,分三個檔次收費,第一檔是用電量不超過180千瓦時實行“基本電價”,第二、三檔實行“提高電價”,具體收費情況如折線圖,

請根據圖像回答下列問題;
(1)當用電量是180千瓦時時,電費是_______________元;
(2)第二檔的用電量范圍是________________________;
(3)“基本電價”是__________________元/千瓦時;
(4)小明家4月份的電費是337.5元,這個月他用電__________________千瓦時?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:CD是經過∠BCA頂點C的一條直線,CA=CB.E,F分別是直線CD上兩點,且∠BEC=∠CFA=∠α.

(1)若直線CD經過∠BCA的內部,且E,F在射線CD上.
①如圖1,若∠BCA=90°,∠α=90°,則BE CF;
②如圖2,若0°<∠BCA<180°,請添加一個關于∠α與∠BCA關系的條件 ,使①中的結論仍然成立,并說明理由;
(2)如圖3,若直線CD經過∠BCA的外部,∠α=∠BCA,請提出關于EF,BE,AF三條線段數量關系的合理猜想:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com