
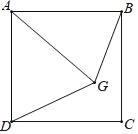
【題目】如圖,點G為正方形ABCD內一點,AB=AG,∠AGB=70°,聯結DG,那么∠BGD=_____度.
【答案】135.
【解析】
根據正方形的性質可得出AB=AD、∠BAD=90°,由AB=AG、∠AGB=70°利用等腰三角形的性質及三角形內角和定理可求出∠BAG的度數,由∠DAG=90°-∠BAG可求出∠DAG的度數,由等腰三角形的性質結合三角形內角和定理可求出∠AGD的度數,再由∠BGD=∠AGB+∠AGD可求出∠BGD的度數.
∵四邊形ABCD為正方形,
∴AB=AD,∠BAD=90°.
∵AB=AG,∠AGB=70°,
∴∠BAG=180°﹣70°﹣70°=40°,
∴∠DAG=90°﹣∠BAG=50°,
∴∠AGD=![]() (180°﹣∠DAG)=65°,
(180°﹣∠DAG)=65°,
∴∠BGD=∠AGB+∠AGD=135°.
故答案為:135.


 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖1,2分別是某款籃球架的實物圖與示意圖,已知底座BC=0.60米,底座BC與支架AC所成的角∠ACB=75°,支架AF的長為2.50米,籃板頂端F點到籃框D的距離FD=1.35米,籃板底部支架HE與支架AF所成的角∠FHE=60°,求籃框D到地面的距離(精確到0.01米)(參考數據:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中數學 來源: 題型:
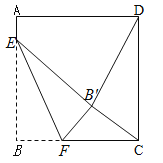
【題目】如圖,正方形ABCD的邊長是16,點E在邊AB上,AE=3,點F是邊BC上不與點B、C重合的一個動點,把△EBF沿EF折疊,點B落在B′處,若△CDB′恰為等腰三角形,則DB′的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】益馬高速通車后,將桃江馬跡塘的農產品運往益陽的運輸成本大大降低。馬跡塘一農戶需要將A,B兩種農產品定期運往益陽某加工廠,每次運輸A,B產品的件數不變,原來每運一次的運費是1200元,現在每運一次的運費比原來減少了300元,A,B兩種產品原來的運費和現在的運費(單位:元∕件)如下表所示:
品種 | A | B |
原來的運費 | 45 | 25 |
現在的運費 | 30 | 20 |
(1)求每次運輸的農產品中A,B產品各有多少件?
(2)由于該農戶誠實守信,產品質量好,加工廠決定提高該農戶的供貨量,每次運送的總件數增加8件,但總件數中B產品的件數不得超過A產品件數的2倍,問產品件數增加后,每次運費最少需要多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了提高學生的漢字書寫能力,某學校連續舉辦了幾屆漢字聽寫大賽,今年經過層層選拔,確定了參加決賽的選手,決賽的比賽規則是每正確聽寫出1個漢字得2分,滿分是100分,下面是根據決賽的成績繪制出的不完整的頻數分布表、扇形統計圖和頻數分布直方圖.
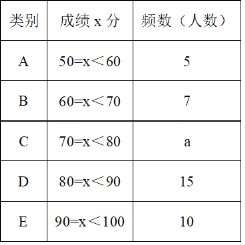
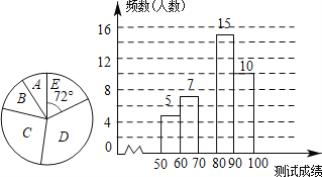
請結合圖表完成下列各題
(1)表中a的值為______,并把頻數分布直方圖補充完整;
(2)學校想利用頻數分布表估計這次決賽的平均成績,請你直接寫出平均成績;
(3)通過與去年的決賽成績進行比較,發現今年各類人數的中位數有了顯著提高,提高了15%以上,求去年各類人數的中位數最高可能是多少?
(4)想從A類學生的3名女生和2名男生中選出兩人進行培訓,直接寫出選中1名男生和1名女生的概率是多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種工業原料,甲倉庫有12噸,乙倉庫有6噸,現需從甲、乙兩倉庫將這種工業原料分別調往A工廠10噸,B工廠8噸,已知從甲倉庫調運1噸原料到A,B兩工廠的運費分別是40元和80元,從乙倉庫調運1噸原料到A,B兩工廠的運費分別是30元和50元.
(1)若總運費為900元,則從甲倉庫調運到A工廠的原料為多少噸?
(2)要使總運費最低,應如何安排調運方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為爭創文明城市,我市交警部門在全市范圍開展了安全使用電瓶車專項宣傳活動.在活動前和活動后分別隨機抽取了部分使用電瓶車的市民,就騎電瓶車戴安全帽情況進行問卷調查,并將兩次收集的數據制成如下統計圖表.

類別 | 人數 | 百分比 |
A | 68 | 6.8% |
B | 245 | b% |
C | a | 51% |
D | 177 | 17.7% |
總計 | c | 100% |
根據以上提供的信息解決下列問題:
(1)a= ,b= c=
(2)若我市約有30萬人使用電瓶車,請分別計算活動前和活動后全市騎電瓶車“都不戴”安全帽的人數.
(3)經過某十字路口,汽車無法繼續直行只可左轉或右轉,電動車不受限制,現有一輛汽車和一輛電動車同時到達該路口,用畫樹狀圖或列表的方法求汽車和電動車都向左轉的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把“有兩條邊和其中一邊的對角對應相等的兩個三角形”叫做“同族三角形”,如圖1,在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B,則△ABC和△ABD是“同族三角形”.
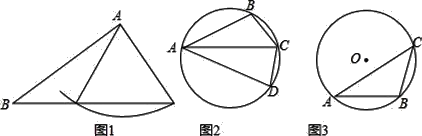
(1)如圖2,四邊形ABCD內接于圓,點C是弧BD的中點,求證:△ABC和△ACD是同族三角形;
(2)如圖3,△ABC內接于⊙O,⊙O的半徑為![]() ,AB=6,∠BAC=30°,求AC的長;
,AB=6,∠BAC=30°,求AC的長;
(3)如圖3,在(2)的條件下,若點D在⊙O上,△ADC與△ABC是非全等的同族三角形,AD>CD,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com