【題目】在一個不透明的盒子中，共有“一白三黑”四個圍棋子，其除顏色外無其他區別．
（1）隨機地從盒子中取出1子，則提出的是白子的概率是多少？
（2）隨機地從盒子中取出1子，不放回再取出第二子，請用畫樹狀或列表的方式表示出所有可能的結果，并求出恰好取出“一黑一白”的概率是多少？
【答案】
（1）解：∵共有“一白三黑”四個圍棋子，
∴提出的是白子的概率是 
（2）解：根據題意列表如下：
白 | 黑1 | 黑2 | 黑3 | |
白 | ﹣ | （白，黑1） | （白，黑2） | （白，黑3） |
黑1 | （黑1，白） | ﹣ | （黑1，黑2） | （黑1，黑3） |
黑2 | （黑2，白） | （黑2，黑1） | ﹣ | （黑2，黑3） |
黑3 | （黑3，白） | （黑3，黑1） | （黑3，黑2） | ﹣ |
∵共有12種等可能的結果數，恰好取出“一黑一白”的情況數有6種，
∴P（ 一黑一白）= 
= 
【解析】（1）已知盒子中共有“一白三黑”四個圍棋子，根據概率公式即可求出提出的是白子的概率。
（2）抓住已知隨機地從盒子中取出1子，不放回再取出第二子，畫出樹狀圖或列表，求出一共有的等可能數，及恰好取出“一黑一白”的情況數，即可求得此概率。
【考點精析】解答此題的關鍵在于理解列表法與樹狀圖法的相關知識，掌握當一次試驗要設計三個或更多的因素時，用列表法就不方便了，為了不重不漏地列出所有可能的結果，通常采用樹狀圖法求概率，以及對概率公式的理解，了解一般地，如果在一次試驗中，有n種可能的結果，并且它們發生的可能性都相等，事件A包含其中的m中結果，那么事件A發生的概率為P（A）=m/n．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】今年兩會提出：隨著城鎮化水平的提高，為了房地產去庫存，國家鼓勵農民進城買房，可享受政府擔保免收利息的惠民政策，小王家購買了一套學區房，首付15萬元后，剩余部分貸款，貸款金額按月分期還款，每月還款數相同，計劃每月還款y萬元，x個月還清貸款，已知y是x的反比例函數，其圖象如圖所示．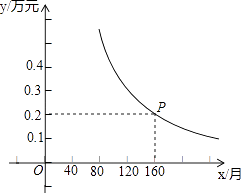
（1）求y與x的函數解析式（關系式），并求小王家購買的學區房的總價是多少萬元？
（2）若計劃80個月還清貸款，則每月應還款多少萬元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知一次函數y1= 
x+b的圖象l與二次函數y2=﹣x2+mx+b的圖象C′都經過點B（0，1）和點C，且圖象C′過點A（2﹣ 
，0）．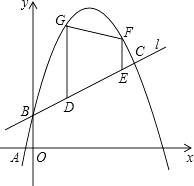
（1）求二次函數的最大值；
（2）設使y2＞y1成立的x取值的所有整數和為s，若s是關于x的方程 
=0的根，求a的值；
（3）若點F、G在圖象C′上，長度為 的線段DE在線段BC上移動，EF與DG始終平行于y軸，當四邊形DEFG的面積最大時，在x軸上求點P，使PD+PE最小，求出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖Rt△ABC中∠BAC=90°，AB=AC，D、E是斜邊BC上兩點，且∠DAE=45°，將△ADC繞點A順時針旋轉90°后，得△AFB，連接EF，下列結論：①△AED≌△AEF；②△ABC的面積等于四邊形AFBD的面積；③BE+DC=DE；④BE2+DC2=DE2；⑤∠DAC=22.5°，其中正確的是（ ）
A. ①②④B. ③④⑤C. ①③④D. ①②⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】四川雅安發生地震后，某校學生會向全校1900名學生發起了“心系雅安”捐款活動，為了解捐款情況，學會生隨機調查了部分學生的捐款金額，并用得到的數據繪制了如下統計圖①和圖②，請根據相關信息，解答下列是問題：
（1）本次接受隨機抽樣調查的學生人數為 ，圖①中m的值是 ；
（2）求本次調查獲取的樣本數據的平均數、眾數和中位數；
（3）根據樣本數據，估計該校本次活動捐款金額為10元的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某日在我國某島附近海域有兩艘自西向東航行的海監船A、B，船在A船的正東方向，且兩船保持20海里的距離，某一時刻兩海監船同時測得在A的東北方向，的北偏東15°方向有一我國漁政執法船C，求此時船C與船B的距離是多少．（結果保留小數點后一位）
參考數據： 
≈1.414， 
≈1.732， 
≈2.236．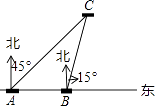
查看答案和解析>>
科目：初中數學 來源： 題型：
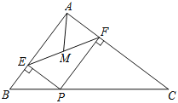
【題目】如圖，在△ABC中，AB=3，AC=4，BC=5，P為邊BC上一動點，PE⊥AB于E，PF⊥AC于F，M為EF中點，則AM的最小值為 ( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖1，AB∥CD，點M為直線AB，CD所確定的平面內的一點，若∠A105，∠M108，請直接寫出∠C的度數 ；
（2）如圖2，AB∥CD，點P為直線AB，CD所確定的平面內的一點，點E在直線CD上，AN平分∠PAB，射線AN的反向延長線交∠PCE的平分線于M，若∠P30，求∠AMC的度數；
（3）如圖3，點P與直線AB，CD在同一平面內，AN平分∠PAB，射線AN的反向延長線交∠PCD的平分線于M，若AMC180
P，求證：AB∥CD．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某風景區內的公路如圖1所示，景區內有免費的班車，從入口處出發，沿該公路開往草甸，途中停靠塔林（上下車時間忽略不計），第一班車上午8點發車，以后每隔10分鐘有一班車從入口處發車，小聰周末到該風景區游玩，上午7：40到達入口處，因還沒到班車發車時間，于是從景區入口處出發，沿該公路步行25分鐘后到達塔林，離入口處的路程
（米）與時間
（分）的函數關系如圖2所示．
（1）求第一班車從入口處到達塔林的時間．
（2）小聰在塔林游玩40分鐘后，想坐班車到草甸，則小聰最早能夠坐上第幾班車？如果他坐這班車到草甸，比他在塔林游玩結束后立即步行到草甸提早了幾分鐘？（假設每一班車速度均相同，小聰步行速度不變）．
（3）若小聰在8：30至8：50之間到達發車站乘坐班車，且到達發車站的時刻是隨機的，則他等車時間不超過3分鐘的概率是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com