
【題目】如圖,正六邊形ABCDEF的邊長為6cm,P是對角線BE上一動點,過點P作直線l與BE垂直,動點P從B點出發且以1cm/s的速度勻速平移至E點.設直線l掃過正六邊形ABCDEF區域的面積為S(cm2),點P的運動時間為t(s),下列能反映S與t之間函數關系的大致圖象是( )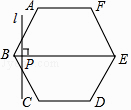
A.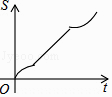
B.
C.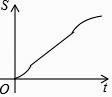
D.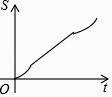
【答案】C
【解析】解:由題意得:BP=t,
如圖1,連接AC,交BE于G,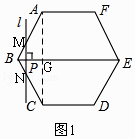
Rt△ABG中,AB=6,∠ABG=60°,
∴∠BAG=30°,
∴BG= ![]() AB=3,
AB=3,
由勾股定理得:AG= ![]() =3
=3 ![]() ,
,
∴AC=2AG=6 ![]() ,
,
當0≤t≤3時,PM= ![]() t,
t,
∴MN=2 ![]() t,
t,
S=S△BMN= ![]() MNPB=
MNPB= ![]() =
= ![]() ,
,
所以選項A和B不正確;
如圖2,當9≤t≤12時,PE=12﹣t,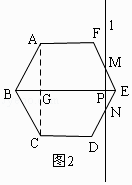
∵∠MEP=60°,
∴tan∠MEP= ![]() ,
,
∴PM= ![]() (12﹣t),
(12﹣t),
∴MN=2PM=2 ![]() (12﹣t),
(12﹣t),
∴S=S正六邊形﹣S△EMN ,
=2× ![]() (AF+BE)×AG﹣
(AF+BE)×AG﹣ ![]() MNPE,
MNPE,
=(6+12)×3 ![]() ﹣
﹣ ![]() ×
× ![]() (12﹣t)(12﹣t),
(12﹣t)(12﹣t),
=54 ![]() ﹣
﹣ ![]() (144﹣24t+t2),
(144﹣24t+t2),
=﹣ ![]() +24
+24 ![]() t﹣90
t﹣90 ![]() ,
,
此二次函數的開口向下,
所以選項C正確,選項D不正確;
故選C.
從給出的圖象中看,中間位置的圖象一致,只要計算兩邊取值中的圖象即可作出判斷;先計算點P從B到G時掃過的面積S,發現是二次函數,且開口向下,可以否定和B,再計算點P從9≤t≤12時掃過的面積為正六邊形的面積﹣△EMN的面積,計算得到一個開口向下的二次函數,由此作判斷.


 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:
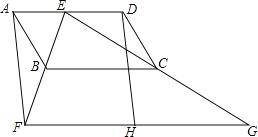
【題目】如圖,四邊形ABCD為平行四邊形,E為AD上的一點,連接EB并延長,使![]() ,連接EC并延長,使
,連接EC并延長,使![]() ,連接
,連接![]() 為FG的中點,連接DH.
為FG的中點,連接DH.
![]() 求證:四邊形AFHD為平行四邊形;
求證:四邊形AFHD為平行四邊形;
![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,∠ABD、∠CDB的平分線BE、DF分別交邊AD、BC于點E、F.
(1)求證:四邊形BEDF是平行四邊形;
(2)當∠ABE為多少度時,四邊形BEDF是菱形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】飲水機原有水的溫度為20℃,通電開機后,飲水機自動開始加熱(此過程中水溫y與開機時間x滿足一次函數關系),當加熱到100℃是自動停止加熱,隨后水溫開始下降(此過程水溫y與開機時間x成反比例關系),當水溫將至20℃時,飲水機又自動開始加熱,…重復上述程序(如圖所示),根據圖中提供的信息,解答下列問題:
(1)當0≤x≤8,求水溫y與開機時間x的函數關系.
(2)求圖中t的值.
(3)在通電后45分鐘飲水機內水溫約為多少度?在通電后60分鐘飲水機內水溫約為多少度?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D在⊙O的直徑AB的延長線上,點C在⊙O上,AC=CD,∠ACD=120°. 
(1)求證:CD是⊙O的切線;
(2)若⊙O的半徑為4,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了了解本校學生采用何種方式上網查找所需要的學習資源,隨機抽取部分學生了解情況,并將統計結果繪制成頻數分布表及頻數分布直方圖. 上網查找學習資源方式頻數分布表
查找方式 | 頻數 | 頻率 |
搜索引擎 | 16 | 32% |
專題網站 | 15 | a |
在線網校 | 4 | 8% |
試題題庫 | 10 | 20% |
其他 | b | 10% |
(1)頻數分布表中a,b的值:a=;b=;
(2)補全頻數分布直方圖; 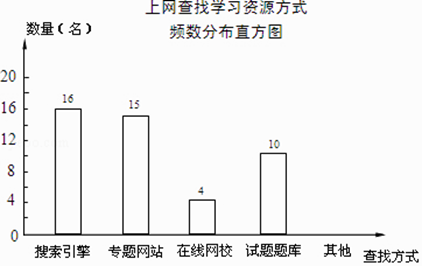
(3)若全校有1000名學生,估計該校利用搜索引擎上網查找學習資源的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古籍《周髀算經》中早有記載“勾三股四弦五”,下面我們來探究兩類特殊的勾股數.通過觀察完成下面兩個表格中的空格(以下a、b、c為Rt△ABC的三邊,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔細觀察,表一中a為大于1的奇數,此時b、c的數量關系是_____________,
a、b、c之間的數量關系是_________________________;
(2)仔細觀察,表二中a為大于4的偶數,此時b、c的數量關系是_____________,
a、b、c之間的數量關系是_________________________;
(3)我們還發現,表一中的三邊長“3,4,5”與表二中的“6,8,10”成倍數關系,表一中的“5,12,13”與表二中的“10,24,26”恰好也成倍數關系……請直接利用這一規律計算:在Rt△ABC中,當![]() ,
,![]() 時,斜邊c的值.
時,斜邊c的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A是雙曲線y= ![]() 在第一象限的分支上的一個動點,連結AO并延長交另一分支于點B,以AB為斜邊做等腰直角△ABC,點C在第四象限.隨著點A的運動,點C的位置也不斷變化,但點C始終在雙曲線y=
在第一象限的分支上的一個動點,連結AO并延長交另一分支于點B,以AB為斜邊做等腰直角△ABC,點C在第四象限.隨著點A的運動,點C的位置也不斷變化,但點C始終在雙曲線y= ![]() (k<0)上運動,則k的值是
(k<0)上運動,則k的值是 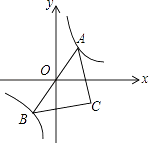
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com