
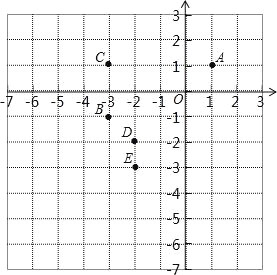
【題目】在同一平面直角坐標系中有6個點:
A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(﹣2,﹣3),F(0,﹣4).
(1)畫出△ABC的外接圓⊙P,則點D與⊙P的位置關系 ;
(2)△ABC的外接圓的半徑= ,△ABC的內切圓的半徑= .
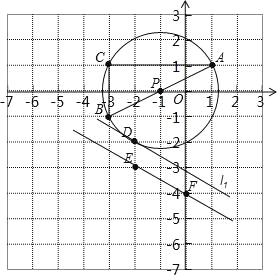
(3)若將直線EF沿y軸向上平移,當它經過點D時,設此時的直線為l1.判斷直線l1與⊙P的位置關系,并說明理由.
【答案】(1)點在圓上
(2)![]() ,3﹣
,3﹣![]() ;
;
(3)直線l1與⊙P相交.
【解析】
試題分析:(1)分別找出AC與BC的垂直平分線,交于點P,即為圓心,求出AP的長即為圓的半徑,畫出圓P,如圖所示,求出D到圓心P的距離,與半徑比較即可做出判斷;
(2)求出三角形ABC的外接圓半徑,內切圓半徑即可;
(3)利用待定系數法求出直線EF的解析式,利用平移性質及題意確定出直線l1解析式,求出圓心P到l1的距離d,與半徑r比較,即可得出直線與圓的位置關系.
試題解析:(1)畫出△ABC的外接圓⊙P,如圖所示,
∵DP=![]() =
=![]() =r,
=r,
∴點D與⊙P的位置關系是點在圓上;
(2)△ABC的外接圓的半徑=![]() ,△ABC的內切圓的半徑=
,△ABC的內切圓的半徑=![]() ;
;
(3)設直線EF解析式為y=kx+b,
把E和F坐標代入得:![]() ,
,
解得:k=﹣![]() ,b=﹣4,
,b=﹣4,
∴直線EF解析式為y=﹣![]() x﹣4,
x﹣4,
由平移性質及題意得:直線l1解析式為y+2=﹣![]() (x+2),即x+2y+6=0,
(x+2),即x+2y+6=0,
∵圓心P(0,﹣1)到直線的距離d=![]() <
<![]() =r,
=r,
∴直線l1與⊙P相交.
故答案為:(1)點在圓上;(2)![]() ;3﹣
;3﹣![]()


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】在一個不透明的布袋中裝有除顏色外其余都相同的紅、黃、藍球共200個,墨墨通過多次摸球試驗后發現,其中摸到紅色球和藍色球的頻率穩定在25%和55%,則口袋中可能有黃球個.
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一大一小的兩個可以自由轉動的轉盤,甲盤被平均分成6等份,乙盤被平均分成4等份,每個轉盤均被涂上紅、黃、藍三種顏色.轉動轉盤,當轉盤停止后,指針指向的顏色即為轉出的顏色.小明與小穎參與游戲:小明轉動甲盤,小穎轉動乙盤.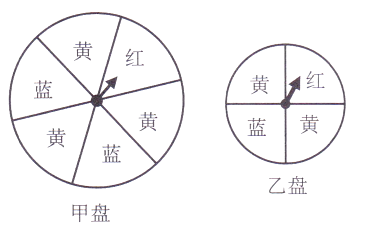
(1)小明轉出的顏色為紅色的概率為;
(2)小明轉出的顏色為黃色的概率為;
(3)小穎轉出的顏色為黃色的概率為;
(4)兩人均轉動轉盤,如果轉出的顏色為紅,則勝出.你認為該游戲公平嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把拋物線y=﹣x2向左平移1個單位,然后向上平移3個單位,則平移后拋物線的解析式為( )
A.y=﹣(x﹣1)2﹣3B.y=﹣(x+1)2﹣3
C.y=﹣(x﹣1)2+3D.y=﹣(x+1)2+3
查看答案和解析>>
科目:初中數學 來源: 題型:
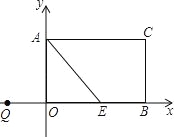
【題目】如圖,矩形AOBC,A(0,3)、B(5,0),點E在OB上,∠AEO=45°,點P從點Q(﹣3,0)出發,沿x軸向右以每秒1個單位長的速度運動,運動時間為t (t≥0)秒.
(1)求點E的坐標;
(2)當∠PAE=15°時,求t的值;
(3)以點P為圓心,PA為半徑的⊙P隨點P的運動而變化,當⊙P與四邊形AEBC的邊(或邊所在的直線)相切時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
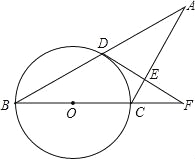
【題目】已知:如圖,△ABC中,AC=BC,以BC為直徑的⊙O交AB于點D,過點D作DE⊥AC于點E,交BC的延長線于點F.
求證:
(1)AD=BD;
(2)DF是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年4月6日,交通運輸部科學研究院對外發布《2017年第一季度中國主要城市騎行報告》,報告顯示,在車均使用次數方面,昆明排名第一,成為“最愛騎共享單車的城市”.目前已經投入昆明的共享單車約有112000輛.將“112000”用科學記數法表示為( )
A.1.12×103
B.1.12×104
C.1.12×105
D.11.2×104
查看答案和解析>>
科目:初中數學 來源: 題型:
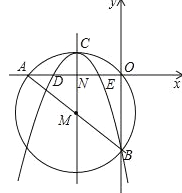
【題目】如圖,在平面直角坐標系中,圓M經過原點O,且與x軸、y軸分別相交于A(﹣8,0),B(0,﹣6)兩點.
(1)求出直線AB的函數解析式;
(2)若有一拋物線的對稱軸平行于y軸且經過點M,頂點C在圓M上,開口向下,且經過點B,求此拋物線的函數解析式;
(3)設(2)中的拋物線交x軸于D、E兩點,在拋物線上是否存在點P,使得S△PDE=![]() S△ABC?若存在,請求出點P的坐標;若不存在,請說明理由.
S△ABC?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com