
【題目】如圖,直線l1對應的函數表達式為y=2x-2,直線l1與x軸交于點D.直線l2:y=kx+b與x軸交于點A,且經過點B,直線l1,l2交于點C(m,2).
(1)求點D,點C的坐標;
(2)求直線l2對應的函數表達式;
(3)求△ADC的面積;
(4)利用函數圖象寫出關于x,y的二元一次方程組![]() 的解.
的解.

【答案】(1) 點D (1,0),點C (2,2);(2) y=-x+4 ;(3)3;(4)![]() .
.
【解析】
(1)把 y=0代入直線l1的解析式即可求出點D的坐標,把C(m,2)代入C(m,2)可求出m的值,從而得出點C的坐標;
(2)根據點C,B在直線l2上,利用待定系數法即可求出;
(3)求出點A坐標,根據三角形面積公式可求出△ADC的面積;
(4) 二元一次方程組 ![]() 的解即兩個二次函數的交點坐標.
的解即兩個二次函數的交點坐標.
解:(1)∵點D是直線l1:y=2x-2與x軸的交點,
∴令y=0,則0=2x-2,
∴x=1,
∴點D的坐標為(1,0),
∵點C在直線l1:y=2x-2上,
∴2=2m-2,
∴m=2,
∴點C的坐標為(2,2).
(2)∵點C(2,2),B(3,1)在直線l2上,
∴![]() 解得
解得![]()
∴直線l2對應的函數表達式為y=-x+4.
(3)∵點A是直線l2與x軸的交點,
∴令y=0,則0=-x+4,
解得x=4,即點A(4,0),
∴AD=4-1=3,
∴S△ADC=![]() ×3×2=3.
×3×2=3.
(4)由題圖可知![]() 的解為
的解為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD的對角線交于點O,下列哪組條件不能判斷四邊形ABCD是平行四邊形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】結合數軸與絕對值的知識回答下列問題:
(1)數軸上表示4和1的兩點之間的距離是 ;表示﹣3和2兩點之間的距離是 ;一般地,數軸上表示數m和數n的兩點之間的距離等于|m﹣n|.如果表示數a和﹣2的兩點之間的距離是3,那么a= ;
(2)若數軸上表示數a的點位于﹣4與2之間,求|a+4|+|a﹣2|的值;
(3)當a取何值時,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?請說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
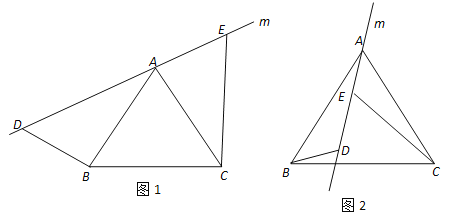
【題目】探索與證明:(1)如圖1,直線m經過正三角形ABC的頂點A,在直線m上取兩點 D,E,使得∠ADB=60°,∠AEC=60°.通過觀察或測量,猜想線段BD,CE與DE之間滿足的數量關系,并予以證明;
(2)將(1)中的直線m繞點A逆時針方向旋轉一個角度到如圖2的位置,并使∠ADB=120°,∠AEC=120°.通過觀察或測量,請直接寫出線段BD,CE與DE之間滿足的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農場去年計劃生產玉米和小麥共200噸.采用新技術后,實際產量為225噸,其中玉米超產5%,小麥超產15%.該農場去年實際生產玉米、小麥各多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是網格圖,每個小正方形的邊長均為1.△ABC(“△”表示“三角形”)是格點三角形(即每個頂點都在小正方形的頂點上),它在坐標平面內平移,得到△PEF,點A平移后落在點P的位置上.
(1)請你在圖中畫出△PEF,并寫出頂點P、E、F的坐標;
(2)說出△PEF是由△ABC分別經過怎樣的平移得到的?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是BC邊上的中線,E是AD的中點,過點A作BC的平行線交BE的延長線于點F,連接CF. 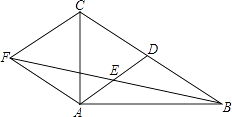
(1)求證:AF=DC;
(2)若AB⊥AC,試判斷四邊形ADCF的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車專賣店銷售![]() ,
,![]() 兩種型號的新能源汽車。上周售出1輛
兩種型號的新能源汽車。上周售出1輛![]() 型車和3輛
型車和3輛![]() 型車,銷售額為96萬元,本周已售出2輛
型車,銷售額為96萬元,本周已售出2輛![]() 型車和1輛
型車和1輛![]() 型車,銷售額為62萬元。
型車,銷售額為62萬元。
(1)求每輛![]() 型車和
型車和![]() 型車的售價各為多少?
型車的售價各為多少?
(2)隨著汽車限購政策的推行,預計下周起![]() ,
,![]() 兩種型號的汽車價格在原有的基礎均有上漲,若
兩種型號的汽車價格在原有的基礎均有上漲,若![]() 型汽車價格上漲m%,
型汽車價格上漲m%,![]() 型汽車價格上漲3m%,則同時購買一臺
型汽車價格上漲3m%,則同時購買一臺![]() 型車和一臺
型車和一臺![]() 型車的費用比漲價前多12%,求
型車的費用比漲價前多12%,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com