
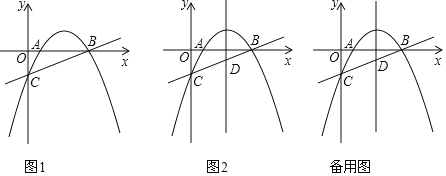
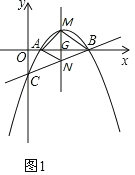
【題目】如圖,直線![]() 與x軸、y軸分別交于BC兩點,拋物線
與x軸、y軸分別交于BC兩點,拋物線![]() 經過B、C兩點,且與x軸交于點A
經過B、C兩點,且與x軸交于點A
(1)求該拋物線的函數表達式;
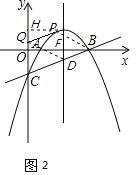
(2)已知點M是第一象限內拋物線上的一個動點,過點M作MN平行于y軸交直線BC于點N,連接AM、BM、AN,求四邊形MANB面積S的最大值,并求出此時點M的坐標;
(3)拋物線的對稱軸交直線BC于點D,若Q為y軸上一點,則在拋物線上是否存在一點P,使得以B、D、P、Q為頂點的四邊形是平行四邊形?若存在,直接寫出點P的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)當t=
;(2)當t=![]() 時,S四邊形MANB的最大值=5,此時點M
時,S四邊形MANB的最大值=5,此時點M![]() ;(3)P坐標為
;(3)P坐標為![]() 或
或![]() 或
或![]() .
.
【解析】
(1)直線![]() 與x軸、y軸的交點為B(5,0),C(0,﹣2),代入拋物線解析式可求出a,c的值;
與x軸、y軸的交點為B(5,0),C(0,﹣2),代入拋物線解析式可求出a,c的值;
(2)設點![]() ,用含t的代數式表示四邊形MANB的面積,得到S與t的函數關系式,利用二次函數最大值求出t的值;
,用含t的代數式表示四邊形MANB的面積,得到S與t的函數關系式,利用二次函數最大值求出t的值;
(3)存在,分BD為平行四邊形的邊或對角線進行分類討論.
解:(1)由![]() x﹣2=0得x=5,
x﹣2=0得x=5,
∴B(5,0),令x=0,得y=﹣2,
∴C(0,﹣2),
由題意得:![]() ,
,
解得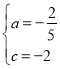 ,
,
∴拋物線解析式為 ![]() .
.
(2)如圖1,設![]() ,
,
![]()
S四邊形MANB=S△AMN+S△BMN
=![]() AGMN+
AGMN+![]() BGMN
BGMN
=![]() MN(AG+BG)
MN(AG+BG)
=![]() MNAB
MNAB
=![]() ×4(
×4(![]() t2+2t)
t2+2t)
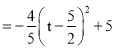
∵![]() <0,
<0,
∴當t=![]() 時,S四邊形MANB的最大值=5,此時點M
時,S四邊形MANB的最大值=5,此時點M![]() .
.
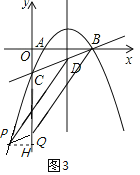
(3)存在.由為 ![]() ,
,
∴拋物線對稱軸x=3.對稱軸交x軸于F,
①以BD為邊,PQ在BC上方,如圖2,D(3,![]() ),F(3,0),
),F(3,0),
∵四邊形BDQP是平行四邊形,∴BD∥PQ,BD=PQ,
過點P作PH⊥y軸于H,
∴∠PHQ=∠BFD=90°,∠PQH=∠BCO=∠BDF,
∴△PQH≌△BDF,
∴PH=BF=2,HQ=FD=![]() ,
,
∴P(2,![]() ).
).
②以BD為邊,PQ在BC下方,如圖3,仿照①可求得P![]() ,
,
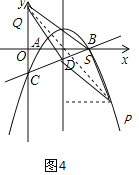
③以BD為平行四邊形對角線,如圖4,設BD中點為S,則S![]() ,
,
∵BPDQ是平行四邊形,
∴BD與PQ互相平分,
∴SQ=SP,
∴S是PQ中點,
設![]() ,
,
∴![]() ,
,
∴a=8,
∴P(8,![]() )
)
綜上所述,P坐標為![]() 或
或![]() 或
或![]() .
.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
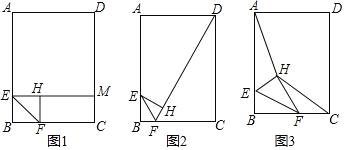
【題目】如圖,點E,F分別在矩形ABCD的邊AB,BC上,連接EF,將△BEF沿直線EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如圖1,當∠BEF=45°時,EH的延長線交DC于點M,求HM的長;
(2)如圖2,當FH的延長線經過點D時,求tan∠FEH的值;
(3)如圖3,連接AH,HC,當點F在線段BC上運動時,試探究四邊形AHCD的面積是否存在最小值?若存在,求出四邊形AHCD的面積的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c經過點(﹣1,0),以下結論:①2a+b>0;②a+c<0;③4a+2b+c>0;④b2﹣5a2>2ac.其中正確的是( )
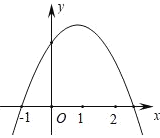
A. ①②B. ③④C. ②③④D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小方與小輝在玩軍棋游戲,他們定義了一種新的規則,用軍棋中的“工兵”、“連長”、“地雷”比較大小,共有6個棋子,分別為1個“工兵”,2個“連長”,3個“地雷”游戲規則如下:①游戲時,將棋反面朝上,兩人隨機各摸一個棋子進行比賽,先摸者摸出的棋不放回;②“工兵”勝“地雷”,“地雷”勝“連長”,“連長”勝“工兵”;③相同棋子不分勝負.
(1)若小方先摸,則小方摸到“排長”的事件是 ;若小方先摸到了“連長”,小輝在剩余的5個棋子中隨機摸一個,則這一輪中小方勝小輝的概率為 .
(2)如果先拿走一個“連長”,在剩余的5個棋子中小方先摸一個棋子,然后小輝在剩余的4個棋子中隨機摸一個,求這一輪中小方獲勝的概率 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=x+1的圖象l與y軸交于點C,A1的坐標為(1,0),點B1在直線l上,且A1B1平行于y軸,連接CA1、OB1交于點P1,過點A1作A1B2∥OB1交直線l于點B2,過點B1作B1A2∥CA1交x軸于點A2,A1B2與B1A2交于點P2,……,按此進行下去,則點P2019的坐標為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某教學活動小組選定測量小山上方某信號塔PQ的高度,他們在A處測得信號塔頂端P的仰角為45°,信號塔低端Q的仰角為31°,沿水平地面向前走100米到處,測得信號塔頂端P的仰角為68°.求信號塔PQ的高度.(結果精確到0.1米.參考數據:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
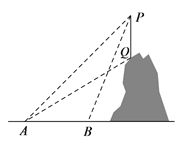
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,已知點A(﹣3,0),B(0,4),對△OAB連續作旋轉變換,依次得到△1,△2,△3,△4,…,則△2019的直角頂點的坐標為( )
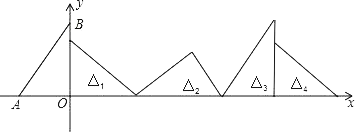
A. (8076,0)B. (8064,0)C. (8076,![]() )D. (8064,
)D. (8064,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近幾年購物的支付方式日益增多,某數學興趣小組就此進行了抽樣調查.調查結果顯示,支付方式有:A微信、B支付寶、C現金、D其他,該小組對某超市一天內購買者的支付方式進行調查統計,得到如下兩幅不完整的統計圖.

請你根據統計圖提供的信息,解答下列問題:
(1)本次一共調查了多少名購買者?
(2)請補全條形統計圖;在扇形統計圖中A種支付方式所對應的圓心角為 度.
(3)若該超市這一周內有1600名購買者,請你估計使用A和B兩種支付方式的購買者共有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,按以下步驟作圖:①以A為圓心,任意長為半徑作弧,分別交AB,AD于點M,N;②分別以M,N為圓心,以大于![]() MN的長為半徑作弧,兩弧相交于點P;③作AP射線,交邊CD于點Q,若DQ=2QC,BC=3,則平行四邊形ABCD周長為________.
MN的長為半徑作弧,兩弧相交于點P;③作AP射線,交邊CD于點Q,若DQ=2QC,BC=3,則平行四邊形ABCD周長為________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com